��Ŀ����
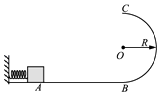
����Ŀ����ͼ��ʾ������ΪL������ϸ��һ�˹̶���O�㣬��һ��˩סһ������Ϊm��С����O�����·�A��̶�һ������ֱ�洹ֱ�Ķ��ӣ�ϸ���ڶ��ӵ��Ҳࣩ������͵��С��һˮƽ���ҵij��ٶȣ�ʹС��ǡ���ܾ���Բ���˶�����ߵ㣬����һ���������������ٶ�Ϊg��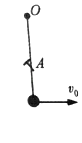
��1����С����ߵ���ٶ�v��С��
��2����С������͵��õij��ٶ�v0��С��
��3����С��ص���͵�λ��ʱ����ͬѧ��Ϊ������С��Խ������Խ���ϣ�����ͬѧ��Ϊ������С��ԽԶ����Խ���ϣ���ͨ������˵����ͬ��˭�Ĺ۵㣮
���𰸡�
��1��
С��ǡ����ͨ����ߵ㣬��mg= ![]() �����v=
�����v= ![]()
��С����ߵ���ٶ�v��СΪ ![]() ��
��
��2��
����ߵ㵽��͵㣬���ö��ܶ�����֪2mgL= ![]() �����
����� ![]()
��С������͵��õij��ٶ�v0��СΪ ![]()
��3��
�趤�ӵ�С��ľ���Ϊr������ţ�ٵڶ����ɿ�֪F��mg= ![]() �����F=mg+
�����F=mg+ ![]() ����rԽС������Խ������Խ���ϣ��ʼ�ͬѧ��ȷ
����rԽС������Խ������Խ���ϣ��ʼ�ͬѧ��ȷ
�𣺼�ͬѧ�۵���ȷ
����������1��С��ǡ����ͨ����ߵ㣬����ߵ㴦ֻ������������ţ�ٵڶ���������ٶȣ���2������ߵ㵽��͵㣬���ö��ܶ�����ó��ٶȣ���3��ͨ��ţ�ٵڶ�����������ӵ����������ж�
�����㾫����������Ĺؼ��������������������֪ʶ����������������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ�����������Լ��Զ��ܶ������ۺ�Ӧ�õ����⣬�˽�Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ�

 �������ͬ������ϵ�д�
�������ͬ������ϵ�д�