题目内容
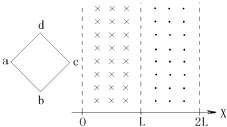
【题目】如图所示,匀强磁场的磁感应强度B=0.5T,边长L=10cm的正方形线圈abcd共200匝,线圈电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO′匀速转动,角速度ω=20rad/s,外电路电阻R=4Ω,求:
(1)计算线圈从图示位置转过60°角时的瞬时感应电动势和交流电压表的示数;
(2)线圈从中性面转过60°角的过程中通过电阻R的电荷量;
(3)线圈转动一周外力所做的功.
【答案】
(1)解:电动势的最大值为:Em=nBSω=200×0.5×0.1×0.1×20=20V
从图示位置开始计时,转过60°角时的瞬时感应电动势为:e=20cos60°=10V
电动势的有效值为:E= ![]() =
= ![]() =10
=10 ![]() V
V
交流电压表的示数为:U= ![]() E=
E= ![]() ×10
×10 ![]() =8
=8 ![]() V
V
答:线圈从图示位置转过60°角时的瞬时感应电动势10V,交流电压表的示数8 ![]() V;
V;
(2)解:线圈从中性面转过60°角的过程中通过电阻R的电荷量为:
q=n ![]() =n
=n ![]() =200×
=200× ![]() =0.1C
=0.1C
答:线圈从中性面转过60°角的过程中通过电阻R的电荷量为0.1C;
(3)解:线圈转动一周外力所做的功等于产生的热量,即:
W=Q= ![]() t=
t= ![]() ×
× ![]() =4π
=4π
答:线圈转动一周外力所做的功为4π.
【解析】(1)先根据Em=NBωS求出最大值,先写出电动势的瞬时表达式,再带入数据求得瞬时值;再根据最大值与有效值的关系求出有效值,根据闭合电路的欧姆定律求出电压表的示数;(2)根据q=n ![]() 求线圈从中性面转过60°角的过程中通过电阻R的电荷量;(3)再由焦耳定律求出热量,由功能关系可得.
求线圈从中性面转过60°角的过程中通过电阻R的电荷量;(3)再由焦耳定律求出热量,由功能关系可得.
【考点精析】掌握周期和频率是解答本题的根本,需要知道周期和频率--周期T:交流电完成一次周期性变化所需的时间;在一个周期内,交流电的方向变化两次;频率f:交流电在1s内完成周期性变化的次数.角频率:ω=2π/T=2πf.

【题目】为了探究加速度与力、质量的关系,甲、乙、丙三位同学分别设计了如图所示的实验装置,小车总质量用M表示(乙图中M包括小车与传感器,丙图中M包括小车和与/J、车固连的滑轮),钩码总质量用m表示.

(1)为便于测量合外力的大小,并得到小车总质量一定时,小车的加速度与所受合外力成正比的结论,下列说法正确的是 .
A.三组实验中只有甲需要平衡摩擦力 |
B.三组实验都需要平衡摩擦力 |
C.三组实验中只有甲需要满足所挂钩码的总质量m远小于小车的总质量M的条件 |
D.三组实验都需要满足所挂钩码的总质量m远小于小车的总质量M的条件 |
(2)若乙、丙两位同学发现某次测量中力传感器和测力计读数相同,通过计算得到小车加速度均为![]() 为当地重力加速度,则乙、丙两人实验时所用小车总质量之比为 ,乙、丙两人实验用的钩码总质量之比为 .
为当地重力加速度,则乙、丙两人实验时所用小车总质量之比为 ,乙、丙两人实验用的钩码总质量之比为 .