题目内容
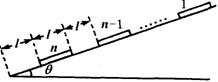 如图所示,有n个相同的货箱停放在倾角为θ的斜面上,每个货箱长皆为l,质量皆为m,相邻两货箱间距离为l,最下端的货箱到斜面底端的距离也为l.已知货箱与斜面间的滑动摩擦力与最大静摩擦力相等.现给第1个货箱一初速度v0.使之沿斜面下滑,在每次发生碰撞后,发生碰撞的货箱都粘合在一起运动,当动摩擦因数为μ时,最后第n个货箱恰好停在斜面底端.求:
如图所示,有n个相同的货箱停放在倾角为θ的斜面上,每个货箱长皆为l,质量皆为m,相邻两货箱间距离为l,最下端的货箱到斜面底端的距离也为l.已知货箱与斜面间的滑动摩擦力与最大静摩擦力相等.现给第1个货箱一初速度v0.使之沿斜面下滑,在每次发生碰撞后,发生碰撞的货箱都粘合在一起运动,当动摩擦因数为μ时,最后第n个货箱恰好停在斜面底端.求:
(1)第1个货箱碰撞前在斜面上运动时的加速度大小;
(2)整个过程中由于碰撞而损失的机械能.
(1)![]() ;(2)
;(2)![]()
解析:
(1)由于第n个货箱被碰后,运动到斜面底端停下,表明货箱沿斜面做减速运动,由牛顿第二定律,得
![]()
解得![]()
(2)加速度与质量无关,说明每次碰后货箱沿斜面下滑的加速度大小均为a,方向沿斜面向上.在整个过程中,序号为1,2,3,…,n的货箱沿斜面下滑的距离分别为nl,(n-1)l,(n-2)l,…,l,因此,除碰撞瞬间外,各货箱由于滑动而产生的摩擦热为![]()
货箱的重力势能的减少量为![]()
全过程中,由能量守恒定律,得
![]() ,则
,则
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
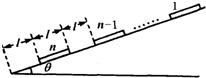 如图所示,有n个相同的货箱沿同一条直线停放在倾角为θ的斜面上,每个货箱长皆为l,质量皆为m,相邻两货箱间距离为l,最下端的货箱到斜面底端的距离也为l.现给第1个货箱一适当的初速度v0,使之沿斜面下滑,在每次发生正碰后(碰撞时间很短),发生碰撞的货箱都粘合在一起运动,当动摩擦因数为μ时,最后第n个货箱恰好停在斜面底端.求:
如图所示,有n个相同的货箱沿同一条直线停放在倾角为θ的斜面上,每个货箱长皆为l,质量皆为m,相邻两货箱间距离为l,最下端的货箱到斜面底端的距离也为l.现给第1个货箱一适当的初速度v0,使之沿斜面下滑,在每次发生正碰后(碰撞时间很短),发生碰撞的货箱都粘合在一起运动,当动摩擦因数为μ时,最后第n个货箱恰好停在斜面底端.求: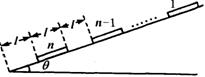

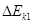 ,第一 次碰撞前的瞬间第一个货箱的动能为
,第一 次碰撞前的瞬间第一个货箱的动能为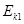 ,求
,求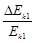 的比值;
的比值;