题目内容
一根内壁光滑的细圆管，形状如图所示，放在竖直平面内，一个球自A口的正上方高h处自由下落．第一次小球恰能抵达B点；第二次落入A口后，自B口射出，恰能再进入A口，则两次小球下的高度之比hl：h2______．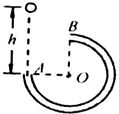
第一次释放时，运动到B点时的速度恰好为零，由机械能守恒得
mgh1=mgR
所以 h1=R
第二次释放后，从B点飞出后做平抛运动，设此时的速度大小为VB，则
水平方向 R=VBt
竖直方向 R=
gt2
解得 VB =
从开始下落到B点的过程中，由机械能守恒得
mgh2=mgR+
mVB2
解得 h2=
R
所以h1：h2=4：5
故答案为：4：5．
mgh1=mgR
所以 h1=R
第二次释放后，从B点飞出后做平抛运动，设此时的速度大小为VB，则
水平方向 R=VBt
竖直方向 R=
| 1 |
| 2 |
解得 VB =
|
从开始下落到B点的过程中，由机械能守恒得
mgh2=mgR+
| 1 |
| 2 |
解得 h2=
| 5 |
| 4 |
所以h1：h2=4：5
故答案为：4：5．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
一根内壁光滑的细圆管，形状如图所示，放在竖直平面内，一个球自A口的正上方高h处自由下落．第一次小球恰能抵达B点；第二次落入A口后，自B口射出，恰能再进入A口，则两次小球下的高度之比hl：h2
