题目内容
1.已知地球半径为R地球表面的重力加速度为g,地球同步卫星距地面的高度为h引力常量G.计算:(1)地球同步卫星周期T
(2)地球密度ρ
分析 (1)同步卫星和地球同步,其周期为地球自转的周期,根据万有引力提供向心力及万有引力和向心力的公式中的角速度公式即可求解;
(2)对于在地面处的物体有万有引力等于物体重力,表示出地球的质量,再根据密度公式求解
解答 解:(1)设地球的质量为M,对于在地面处质量为m的物体有:G$\frac{Mm}{{R}^{2}}$=m g①
设同步卫星的质量为m,则:G$\frac{Mm}{(R+h)^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$(R+h)②
由①②两式解得:T=$\frac{2π(R+h)}{R}\sqrt{\frac{R+h}{g}}$
(2)又因为:ρ=$\frac{M}{\frac{4}{3}π{R}^{3}}$③
由①③两式解得:ρ=$\frac{3g}{4GπR}$
答:(1)同步卫星周期$\frac{2π(R+h)}{R}\sqrt{\frac{R+h}{g}}$(2)地球的密度是$\frac{3g}{4GπR}$
点评 该题为天体运动的典型题型,由万有引力提供向心力,再根据向心力的基本公式求解,解题过程中注意黄金代换式的应用

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.物体在位于同一平面内的三个共点力作用下静止,其中两个力的大小分别为F1=10N,F2=8N.若第三个力与F1的正向夹角为θ,则θ可能为( )
| A. | 60° | B. | 120° | C. | 150° | D. | 180° |
13.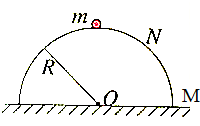 如图所示,半径为R的光滑半圆球固定在水平面上,顶部有一小物体A,今使无初速度放置在球的最高点,现在给其一扰动,则物体将( )
如图所示,半径为R的光滑半圆球固定在水平面上,顶部有一小物体A,今使无初速度放置在球的最高点,现在给其一扰动,则物体将( )
 如图所示,半径为R的光滑半圆球固定在水平面上,顶部有一小物体A,今使无初速度放置在球的最高点,现在给其一扰动,则物体将( )
如图所示,半径为R的光滑半圆球固定在水平面上,顶部有一小物体A,今使无初速度放置在球的最高点,现在给其一扰动,则物体将( )| A. | 沿球面下滑至最低点M | |
| B. | 沿球面下滑至某一点N,便离开球面做斜下抛运动 | |
| C. | 立即离开球面做平抛运动 | |
| D. | 以上说法都不正确 |
10. 如图所示,在足够大的光滑水平面上,一个质量为m=1kg的小球,以速度v0=10m/s向正北方向运动,从t=0时刻起受到向东的恒力F=10N的作用,经过1s后将F的方向改为向西、大小不变.从受力开始到2s末的时间内,下列说法中正确的是( )
如图所示,在足够大的光滑水平面上,一个质量为m=1kg的小球,以速度v0=10m/s向正北方向运动,从t=0时刻起受到向东的恒力F=10N的作用,经过1s后将F的方向改为向西、大小不变.从受力开始到2s末的时间内,下列说法中正确的是( )
 如图所示,在足够大的光滑水平面上,一个质量为m=1kg的小球,以速度v0=10m/s向正北方向运动,从t=0时刻起受到向东的恒力F=10N的作用,经过1s后将F的方向改为向西、大小不变.从受力开始到2s末的时间内,下列说法中正确的是( )
如图所示,在足够大的光滑水平面上,一个质量为m=1kg的小球,以速度v0=10m/s向正北方向运动,从t=0时刻起受到向东的恒力F=10N的作用,经过1s后将F的方向改为向西、大小不变.从受力开始到2s末的时间内,下列说法中正确的是( )| A. | 2s末F做功的功率为0 | B. | 2s内小球的位移为20m | ||
| C. | 第1s内小球的速度变化了10m/s | D. | 第1s内F做功为100J |
1.如图所示,水下光源S向水面A点发射一束复色光线,折射光线分成a、b两束,则下列说法正确的是( )
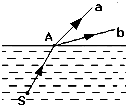

| A. | 在水中a光的速度比b光的速度小 | |
| B. | a光的频率小于b光的频率 | |
| C. | 若a、b两种单色光由玻璃射向空气时,a光的临界角较小 | |
| D. | 若保持入射点A位置不变,将入射光线顺时针旋转,则从水面上方观察,a光先消失 |
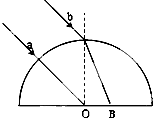 如图所示,一束平行光照射到半球形玻璃砖上,该束光线的边界分别为a和b.已知玻璃砖半径为R,折射率为$\sqrt{2}$,如图所示,下边界a处光线恰好沿半径方向,在O点恰好发生全反射.求:
如图所示,一束平行光照射到半球形玻璃砖上,该束光线的边界分别为a和b.已知玻璃砖半径为R,折射率为$\sqrt{2}$,如图所示,下边界a处光线恰好沿半径方向,在O点恰好发生全反射.求: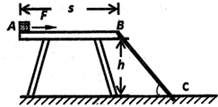 如图所示,小物体质量m=1kg,放在高度为h=5m、长度为S=10m的粗糙水平固定平台的左端A点,小物体与桌面之间的动摩擦因数μ=0.1,在水平平台的右侧有一倾角为53°的斜面BC.现用水平拉力F=3N从静止开始作用于小物体.不计空气阻力.试求:(g取10m/s2)
如图所示,小物体质量m=1kg,放在高度为h=5m、长度为S=10m的粗糙水平固定平台的左端A点,小物体与桌面之间的动摩擦因数μ=0.1,在水平平台的右侧有一倾角为53°的斜面BC.现用水平拉力F=3N从静止开始作用于小物体.不计空气阻力.试求:(g取10m/s2)
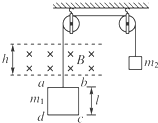 如图所示,线圈abcd每边长l=0.20m,线圈质量m1=0.10kg,电阻R=0.10Ω,砝码质量m2=0.14kg.线圈上方的匀强磁场磁感应强度B=0.5T,方向垂直线圈平面向里,磁场区域的宽度h=l.砝码从某一位置下降,使ab边进入磁场开始做匀速运动,则线圈做匀速运动的速度为4 m/s.(g取10m/s2)
如图所示,线圈abcd每边长l=0.20m,线圈质量m1=0.10kg,电阻R=0.10Ω,砝码质量m2=0.14kg.线圈上方的匀强磁场磁感应强度B=0.5T,方向垂直线圈平面向里,磁场区域的宽度h=l.砝码从某一位置下降,使ab边进入磁场开始做匀速运动,则线圈做匀速运动的速度为4 m/s.(g取10m/s2)