题目内容
11. 如图所示,一束平行光照射到半球形玻璃砖上,该束光线的边界分别为a和b.已知玻璃砖半径为R,折射率为$\sqrt{2}$,如图所示,下边界a处光线恰好沿半径方向,在O点恰好发生全反射.求:
如图所示,一束平行光照射到半球形玻璃砖上,该束光线的边界分别为a和b.已知玻璃砖半径为R,折射率为$\sqrt{2}$,如图所示,下边界a处光线恰好沿半径方向,在O点恰好发生全反射.求:(1)玻璃砖发生全反射的临界角;
(2)光束ab在玻璃砖底产生的两个光斑的距离OB.
分析 (1)已知玻璃砖的折射率,由临界角公式可以求出玻璃砖的临界角.
(2)光线从玻璃砖下表面射出时会发生全反射现象,应用折射定律与几何知识求出光线b从玻璃砖底部射出的位置,然后求出距离.
解答 解:(1)临界角:sinC=$\frac{1}{n}$=$\frac{1}{\sqrt{2}}$,解得:C=45°;
(2)光路图如图所示: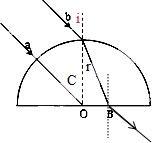
a处光线恰好沿半径方向,在O点恰好发生全反射,
则光线a在玻璃砖底面的入射角等于临界角C,
光线a、b平行,由几何知识可得:i=C=45°,
折射率:n=$\frac{sini}{sinr}$=$\frac{sin45°}{sinr}$=$\sqrt{2}$,
解得:sinr=$\frac{1}{2}$,则:r=30°,
由几何关系得:OB=Rtanr=Rtan30°=$\frac{\sqrt{3}}{3}$R;
答:(1)玻璃砖发生全反射的临界角是45°;
(2)光束ab在玻璃砖底产生的两个光斑的距离OB为$\frac{{\sqrt{3}}}{3}$R.
点评 本题要掌握光的折射定律及全反射临界角公式sinC=$\frac{1}{n}$,要注意分析发应全反射光线的边界的确定,作出光路图即可求解.

练习册系列答案
相关题目
2.将一物体以20m/s的速度竖直向上抛出,则物体上升的最大高度是( )
| A. | 2m | B. | 20m | C. | 15m | D. | 25m |
16. 如图所示,质量为m的物块,沿着半径为R的半球形金属壳内壁滑下,半球形金属壳竖直固定放置,开口向上,滑到最低点时速度大小为v,若物体与球壳之间的摩擦因数为μ,则物体在最低点时,下列说法正确的是( )
如图所示,质量为m的物块,沿着半径为R的半球形金属壳内壁滑下,半球形金属壳竖直固定放置,开口向上,滑到最低点时速度大小为v,若物体与球壳之间的摩擦因数为μ,则物体在最低点时,下列说法正确的是( )
 如图所示,质量为m的物块,沿着半径为R的半球形金属壳内壁滑下,半球形金属壳竖直固定放置,开口向上,滑到最低点时速度大小为v,若物体与球壳之间的摩擦因数为μ,则物体在最低点时,下列说法正确的是( )
如图所示,质量为m的物块,沿着半径为R的半球形金属壳内壁滑下,半球形金属壳竖直固定放置,开口向上,滑到最低点时速度大小为v,若物体与球壳之间的摩擦因数为μ,则物体在最低点时,下列说法正确的是( )| A. | 受到向心力为mg+m$\frac{{v}^{2}}{R}$ | B. | 受到的摩擦力为μm(g+$\frac{{v}^{2}}{R}$) | ||
| C. | 受到的摩擦力为μmg$\frac{{v}^{2}}{R}$ | D. | 受到的合力方向竖直向上 |
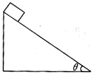 如图所示,质量为m的物体沿倾角为θ,长为l的固定光滑斜面从顶端由静止下滑到底端,则在此过程中重力做的功为mglsinθ,重力的平均功率为$mgsinθ\sqrt{\frac{glsinθ}{2}}$.,滑到底端时重力的瞬时功率为$mgsinθ\sqrt{2glsinθ}$,合外力做的功为mglsinθ.
如图所示,质量为m的物体沿倾角为θ,长为l的固定光滑斜面从顶端由静止下滑到底端,则在此过程中重力做的功为mglsinθ,重力的平均功率为$mgsinθ\sqrt{\frac{glsinθ}{2}}$.,滑到底端时重力的瞬时功率为$mgsinθ\sqrt{2glsinθ}$,合外力做的功为mglsinθ.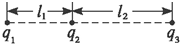 如图所示,q1、q2、q3分别表示在一条直线上的三个点电荷,已知q1与q2之间的距离为l1,q2与q3之间的距离为l2,且每个电荷在电场力作用下都处于平衡状态.如果q2为正电荷,则q1为负电荷,q3为负电荷.
如图所示,q1、q2、q3分别表示在一条直线上的三个点电荷,已知q1与q2之间的距离为l1,q2与q3之间的距离为l2,且每个电荷在电场力作用下都处于平衡状态.如果q2为正电荷,则q1为负电荷,q3为负电荷.