题目内容
12.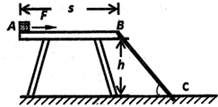 如图所示,小物体质量m=1kg,放在高度为h=5m、长度为S=10m的粗糙水平固定平台的左端A点,小物体与桌面之间的动摩擦因数μ=0.1,在水平平台的右侧有一倾角为53°的斜面BC.现用水平拉力F=3N从静止开始作用于小物体.不计空气阻力.试求:(g取10m/s2)
如图所示,小物体质量m=1kg,放在高度为h=5m、长度为S=10m的粗糙水平固定平台的左端A点,小物体与桌面之间的动摩擦因数μ=0.1,在水平平台的右侧有一倾角为53°的斜面BC.现用水平拉力F=3N从静止开始作用于小物体.不计空气阻力.试求:(g取10m/s2)(1)如果使小物体能到达桌子边缘B,水平力F至少作用多少时间?
(2)如果使小物体的落地点恰为斜面的底端C,则水平力F作用多少距离?
(3)请写出小物体平抛的水平距离X与水平力F作用距离L(L不大于10m)的关系式.
分析 (1)根据牛顿运动定律知加速度,根据匀变速直线运动规律知位移,根据动能定理列式求时间;
(2)根据平抛运动和动能定理列方程解F作用的距离;
(3)根据平抛运动和动能定理列方程解得.
解答 解:(1)据牛顿运动定律知F作用时的加速度为a=$\frac{F-f}{m}$=$\frac{3-0.1×1×10}{1}$=2m/s2
设F作用的时间为t,根据动能定理知
Fx′-fS=0
即F$•\frac{1}{2}a{t}^{2}$-μmgs=0
解得t′=$\sqrt{\frac{10}{3}}$s
(2)物块离开B后做平抛运动,根据平抛运动规律知
h=$\frac{1}{2}g{t}^{2}$
x=vBt=$\frac{h}{tan53°}$
解得vB=3.75m/s
根据动能定理知Fx2--μmgs=$\frac{1}{2}m{v}_{B}^{2}$-0
解得x2=8m
(3)根据动能定理知
FL-μmgS=$\frac{1}{2}m{v}_{B}^{2}$-0
X=vBt
Xtan53°=$\frac{1}{2}g{t}^{2}$
联立得X=$\frac{4tan53°(FL-μmgS)}{mg}$
答:(1)如果使小物体能到达桌子边缘B,水平力F至少作用$\sqrt{\frac{10}{3}}$s;
(2)如果使小物体的落地点恰为斜面的底端C,则水平力F作用8m;
(3)小物体平抛的水平距离X与水平力F作用距离L(L不大于10m)的关系式X=$\frac{4tan53°(FL-μmgS)}{mg}$
点评 本题为平抛运动与动能定理结合的题目,要注意正确平抛运动的规律,将平抛运动分解为水平和竖直两个方向进行研究,综合性强,要求学生熟练记忆相关的公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.将一物体以20m/s的速度竖直向上抛出,则物体上升的最大高度是( )
| A. | 2m | B. | 20m | C. | 15m | D. | 25m |
7.在奥运比赛项目中,高台跳水是我国运动员的强项.质量为m的跳水运动员入水后受到水的阻力而竖直向下做减速运动,设水对他的阻力大小恒为F.那么在他减速下降深度为h的过程中,下列说法错误的是(g为当地的重力加速度)( )
| A. | 他的动能减少了Fh | B. | 他的重力势能减少了mgh | ||
| C. | 他的动能减少了(F-mg)h | D. | 他的机械能减少了Fh |
17.关于功率概念,下列说法中正确的是( )
| A. | 力对物体做的功越多,力做功的功率越大 | |
| B. | 功率是描述物体做功快慢的物理量 | |
| C. | 从公式P=Fv可知道汽车的发动机功率一定时,牵引力与运动速度成反比 | |
| D. | 当轮船航行时,如果牵引力与阻力相等时合外力为零,此时发动机的实际功率为零 |
4.一定质量的0℃的冰熔化成0℃的水时其分子动能之和Ek与分子势能之和Ep及物体内能E的变化情况为( )
| A. | Ek变大,Ep变大,E变大 | B. | Ek变小,Ep变小,E变小 | ||
| C. | Ek不变,Ep变大,E变大 | D. | Ek不变,Ep变小,E变小 |
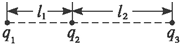 如图所示,q1、q2、q3分别表示在一条直线上的三个点电荷,已知q1与q2之间的距离为l1,q2与q3之间的距离为l2,且每个电荷在电场力作用下都处于平衡状态.如果q2为正电荷,则q1为负电荷,q3为负电荷.
如图所示,q1、q2、q3分别表示在一条直线上的三个点电荷,已知q1与q2之间的距离为l1,q2与q3之间的距离为l2,且每个电荷在电场力作用下都处于平衡状态.如果q2为正电荷,则q1为负电荷,q3为负电荷. 如图,Q为一个原来静止在光滑水平面上的物体,其DB段为一半径为R的光滑圆弧轨道,AD段为一长度为L=R的粗糙水平轨道,二者相切于D点,D在圆心O的正下方,整个轨道位于同一竖直平面内.物块P的质量为m(可视为质点),P与AD间的动摩擦因数μ=0.1,物体Q的质量为M=2m,重力加速度为g.
如图,Q为一个原来静止在光滑水平面上的物体,其DB段为一半径为R的光滑圆弧轨道,AD段为一长度为L=R的粗糙水平轨道,二者相切于D点,D在圆心O的正下方,整个轨道位于同一竖直平面内.物块P的质量为m(可视为质点),P与AD间的动摩擦因数μ=0.1,物体Q的质量为M=2m,重力加速度为g.