题目内容

【题目】如图所示,绷紧的传送带与水平面的夹角θ=30°,传送带在电动机的带动下,始终保持v0=2m/s的速率运行,现把一质量为m=10kg的工件(可看作质点)轻轻放在传送带的底端,工件与传送带之间的动摩擦因数μ= ,经过时间t=1.9s,工件被传送到顶端,g取10m/s2。求:

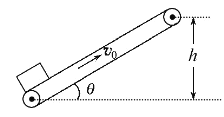
（1）物块刚开始运动时的加速度

（2）传送带的长度

【答案】(1) (2)

【解析】

(1)对物块受力分析，根据牛顿第二定律求物块刚开始运动时的加速度；

(2)由运动学公式求解物块与传送带共速的时间，共速后做匀速运动，根据运动学公式求解两个过程的位移即为传送带的长度.

(1)物块刚开始运动时相对于传送带向下运动，受到向上的滑动摩擦力，滑动摩擦力大小.

重力沿传送带向下的分力mgsin30°=50N

根据牛顿第二定律有：f-mgsin30°=ma

即

(2)设经时间t1工件与传送带共速，

速度相等后，由于mgsin30°＜f，工件和传送带一起做匀速运动，

匀速运动的时间

传送带的长度为

练习册系列答案
相关题目

【题目】放在水平地面上的一物块，受到方向不变的水平推力F的作用，F的大小与时间t的关系和物块速度v与时间t的关系如图所示。取重力加速度g=10 m/s2。由此两图线可以求得物块的质量m和物块与地面之间的动摩擦因数μ分别为（ ）

A. m＝0.5 kg B. m＝1.5 kg

C. μ＝0.4 D. μ＝2/15

【题目】如图所示，一个可视为质点的物体从高为h=0.8m的光滑斜面顶端由静止开始下滑,物体经过A点时速率变化可忽略不计，滑上传送带A端的瞬时速度为vA,到达B端的瞬时速度设为vB,水平传送带A、B两端相距x=6m,物体与传送带间的动摩擦因数μ=0.1,取g=10m/s2,下列说法中正确的是( )

A. 物体滑上传送带A端的瞬时速度vA=4m/s

B. 若传送带不动，物体到达B端的瞬时速度vB=2m/s

C. 若传送带逆时针匀速转动,vB一定小于2m/s

D. 若传送带顺时针匀速转动,vB一定大于2m/s

【题目】如图所示，物体的质量m=10kg，与水平地面间的动摩擦因数为μ=0.5，在倾角为37°，F=50N的恒力作用下，由静止开始匀加速直线运动，求：

（1）物体做匀加速直线运动时的加速度大小；

（2）4s末物体的速度大小？

（3）4s末撤去拉力后，物体还能在水平地面上滑多远？（g=10m/s2，sin37°=0.6，cos37°=0.8）

【题目】如图所示，图中的实线是一列正弦波在某一时刻的波形曲线，经过0.5s后，其波形如图中的虚线所示，该波的周期T大于0.5s，下列说法正确的是

A. 如果这列波往左传播，这列波的周期为2s

B. 如果这列波往左传播，这列波的传播速度为0.36m/s

C. 如果这列波往右传播，碰到尺寸为20cm的障碍物，能发生明显衍射现象

D. 如果这列波往右传播，碰到频率为1.5Hz的简谐横波能够发生干涉现象

【题目】在如图所示的电路中，线圈中的自感系数很大，且其直流电阻可以忽略不计．D1和D2是两个完全相同的小灯泡，在开关S的闭合和断开的过程中（灯丝不会断），D1和D2亮度的变化情况是（　　）

A. S闭合，D1很亮且亮度不变，D2逐渐变亮，最后两灯一样亮；S断开，D2立即灭，D1逐渐变亮

B. S闭合，D1不亮，D2很亮；S断开，D2立即灭

C. S闭合，D1和D2同时亮，而后D1灭，D2亮度不变：S断开，D2立即灭，D1亮一下才灭

D. S闭合，D1和D2同时亮，后D1逐渐熄灭，D2则逐渐变得更亮；S断开，D2立即灭，D1亮一下后才灭

【题目】关于惯性和牛顿第三定律的理解，下列说法正确的是　　

A. “嫦娥一号”卫星在地球上的惯性与它绕月球飞行时的惯性是不相同的燃料消耗忽略不计

B. 作用力和反作用力同时产生，同时消失，不同时变化

C. 各种机床和发电机的底座做得很笨重，目的是增大惯性

D. 两物体只有处于相对静止时，它们之间的作用力和反作用力的大小才相等

【题目】在“油膜法估测油酸分子的大小”实验中，

(1)关于下列实验步骤：

①往边长约为40 cm的浅盘里倒入约2 cm深的水，待水面稳定后将适量的痱子粉均匀地撒在水面上。

②用注射器将事先配好的油酸酒精溶液滴一滴在水面上，待薄膜形状稳定。

③将画有油膜形状的玻璃板平放在坐标纸上，计算出油膜的面积，根据油酸的体积和面积计算出油酸分子直径的大小。

④用注射器将事先配好的油酸酒精溶液一滴一滴地滴入量筒中，记下量筒内每增加一定体积 时的滴数，由此计算出一滴油酸酒精溶液的体积。

⑤将玻璃板放在浅盘上，然后将油膜的形状用彩笔描绘在玻璃板上。

完成下列填空：

上述步骤中，正确的顺序是__________。(填写步骤前面的数字)

（2）油酸酒精溶液的浓度为每1 000 mL油酸酒精溶液中有油酸0.6 mL，现用滴管向量筒内滴加50滴上述溶液，量筒中的溶液体积增加了1 mL，若把一滴这样的油酸酒精溶液滴入足够大盛水的浅盘中，由于酒精溶于水，油酸在水面展开，稳定后形成的油膜的形状如图所示。若每一小方格的边长为25 mm，试问：

这种估测方法是让油酸尽可能地在水面上散开，则形成的油膜可视为___________油膜，这层油膜的厚度可视为油酸分子的___________。图中油酸膜的面积为________m2；估测出油酸分子的直径是________m。(结果保留两位有效数字)

【题目】如图所示，在竖直平面内有一光滑圆形轨道，空间存在一竖直向上的匀强电场，一带正电的小球可在轨道内做圆周运动，且电量保持不变，则下列说法中正确的是（ ）

A. 小球在最低点B的动能一定最大

B. 小球在最高点A的电势能一定最小

C. 小球在与圆心O点等高的C点对轨道的压力可能为零

D. 小球在最低点B的机械能一定最小

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网