题目内容
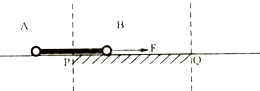 A、B是两个质量均为m=1kg的球,两球由长为L=4m的轻杆相连组成系统.水平面上的P、Q两点间是一段长度为4.5m的租糙面,其余段表面光滑,球A、B与PQ面的动摩擦因数均为μ=0.2.最初,A和B分别静止在P点两侧,离P点的距离均为x0=2m,若视球为质点,不计轻秆质量,对B球施加向右的拉力F=4N,求:
A、B是两个质量均为m=1kg的球,两球由长为L=4m的轻杆相连组成系统.水平面上的P、Q两点间是一段长度为4.5m的租糙面,其余段表面光滑,球A、B与PQ面的动摩擦因数均为μ=0.2.最初,A和B分别静止在P点两侧,离P点的距离均为x0=2m,若视球为质点,不计轻秆质量,对B球施加向右的拉力F=4N,求:(1)A球经过P点时,系统的速度大小为多少?
(2)当A球经过P点时立即撤去F,最后AB球静止.求A球静止时离Q点多远以及A球从开始运动到静止所需的时间.(g=10m/s2,
| 2 |
分析:(1)对系统研究,根据牛顿第二定律求出系统的加速度,结合速度位移公式求出A球经过P点时,系统的大小.
(2)对整体研究,根据牛顿第二定律求出系统在AB间运动时的加速度,根据速度位移公式求出小球B运动到Q点的速度,判断B球能否通过Q点.若能通过,根据牛顿第二定律求出B球滑过Q点后系统的加速度,结合速度位移公式求出继续滑行的距离,从而求出A球静止时离Q点的距离.结合运动学公式分别求出三段过程的时间,从而得出总时间.
(2)对整体研究,根据牛顿第二定律求出系统在AB间运动时的加速度,根据速度位移公式求出小球B运动到Q点的速度,判断B球能否通过Q点.若能通过,根据牛顿第二定律求出B球滑过Q点后系统的加速度,结合速度位移公式求出继续滑行的距离,从而求出A球静止时离Q点的距离.结合运动学公式分别求出三段过程的时间,从而得出总时间.
解答:解:(1)设系统开始运动时加速度大小为a1,由牛顿运动定律,得:a1=
…①
A球经过P点时速度为v1,则有:v12=2a1x0…②
由 ①②求得:v1=
=2m/s…③
(2)A、B在P、Q间运动时加速度大小为a2,有:a2=
=μg…④
若B继续滑行x1,运动到Q点的速度为v2:v22-v12=-2a2x2…⑤
由④⑤得:v2=
=
>0…⑥
由v2>0得,B球将通过Q点
当B球滑过Q点后.加速度大小为a3,由牛顿运动定律,得:a3=
=
…⑦
设系统继续滑行x2后静止,则:x2=
…⑧
由⑦⑧得:x2=1m
即AQ间距离为:xPQ-x1-x2=3m…⑨
由牛顿运动定律及运动学公式,得x0=
a1t12…⑩
x1=v1t2-
a2t22…(11)
t3=
…(12)
由⑩(11)(12)式得:t=t1+t2+t3=3+
=3.85s
答:(1)A球经过P点时,系统的速度大小为2m/s.
(2)A球静止时离Q点3m,A球从开始运动到静止所需的时间为3.85s.
| F-μmg |
| 2m |
A球经过P点时速度为v1,则有:v12=2a1x0…②
由 ①②求得:v1=
2
|
(2)A、B在P、Q间运动时加速度大小为a2,有:a2=
| 2μmg |
| 2m |
若B继续滑行x1,运动到Q点的速度为v2:v22-v12=-2a2x2…⑤
由④⑤得:v2=
| v12-2a2x2 |
| 2 |
由v2>0得,B球将通过Q点
当B球滑过Q点后.加速度大小为a3,由牛顿运动定律,得:a3=
| μmg |
| 2m |
| μg |
| 2 |
设系统继续滑行x2后静止,则:x2=
| v22 |
| 2a3 |
由⑦⑧得:x2=1m
即AQ间距离为:xPQ-x1-x2=3m…⑨
由牛顿运动定律及运动学公式,得x0=
| 1 |
| 2 |
x1=v1t2-
| 1 |
| 2 |
t3=
| v2 |
| a3 |
由⑩(11)(12)式得:t=t1+t2+t3=3+
| ||
| 2 |
答:(1)A球经过P点时,系统的速度大小为2m/s.
(2)A球静止时离Q点3m,A球从开始运动到静止所需的时间为3.85s.
点评:解决本题的关键理清系统在整个过程中的运动情况,结合牛顿第二定律和运动学公式灵活求解.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
 如图,粗糙斜面与光滑水平面通过光滑小圆弧平滑连接,斜面倾角θ=37°,A、B是两个质量均为m=1kg的小滑块(可看作质点),B的左端连接一轻质弹簧.若滑块A在斜面上受到F=4N,方向垂直斜面向下的恒力作用时,恰能沿斜面匀速下滑.现撤去F,让滑块A从斜面上,距斜面底端L=1m处,由静止开始下滑.取g=10m/s2,sin37°=0.6,cos37°=0.8.
如图,粗糙斜面与光滑水平面通过光滑小圆弧平滑连接,斜面倾角θ=37°,A、B是两个质量均为m=1kg的小滑块(可看作质点),B的左端连接一轻质弹簧.若滑块A在斜面上受到F=4N,方向垂直斜面向下的恒力作用时,恰能沿斜面匀速下滑.现撤去F,让滑块A从斜面上,距斜面底端L=1m处,由静止开始下滑.取g=10m/s2,sin37°=0.6,cos37°=0.8. (2013?辽宁一模)如图所示,粗糙斜面与水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾角α=37°,水平面的M到N段是长度L1=0.3m的粗糙平面,N点的右边是光滑的.A、B是两个质量均为m=1kg的小滑块(可看作质点),置于N点处的C是左端附有胶泥的薄板(质量不计),D是两端分别与B和C连接的轻质弹簧,滑块A与斜面和与水平面MN段的动摩擦因数相同.当滑块A置于斜面上且受到大小F=4N、方向垂直斜面向下的恒力作用时,恰能向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L2=1m处由静止下滑(取g=10m/s2,sin37°=0.6,cos37°=0.8),求:滑块A与C接触并粘连在一起后,两滑块与弹簧所构成的系统在相互作用的过程中,弹簧的最大弹性势能.
(2013?辽宁一模)如图所示,粗糙斜面与水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾角α=37°,水平面的M到N段是长度L1=0.3m的粗糙平面,N点的右边是光滑的.A、B是两个质量均为m=1kg的小滑块(可看作质点),置于N点处的C是左端附有胶泥的薄板(质量不计),D是两端分别与B和C连接的轻质弹簧,滑块A与斜面和与水平面MN段的动摩擦因数相同.当滑块A置于斜面上且受到大小F=4N、方向垂直斜面向下的恒力作用时,恰能向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L2=1m处由静止下滑(取g=10m/s2,sin37°=0.6,cos37°=0.8),求:滑块A与C接触并粘连在一起后,两滑块与弹簧所构成的系统在相互作用的过程中,弹簧的最大弹性势能. 如图所示,粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾角α=37°,A、B是两个质量均为 m=1㎏的小滑块(可视为质点),C为左端附有胶泥的质量不计的薄板,D为两端分别连接B和C的轻质弹簧.当滑块A置于斜面上且受到大小F=4N,方向垂直斜面向下的恒力作用时,恰能向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L=1m处由静止下滑,若g取10m/s2,sin37°=0.6,cos37°=0.8.
如图所示,粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾角α=37°,A、B是两个质量均为 m=1㎏的小滑块(可视为质点),C为左端附有胶泥的质量不计的薄板,D为两端分别连接B和C的轻质弹簧.当滑块A置于斜面上且受到大小F=4N,方向垂直斜面向下的恒力作用时,恰能向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L=1m处由静止下滑,若g取10m/s2,sin37°=0.6,cos37°=0.8.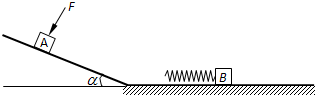 如图所示,粗糙斜面其倾角为α,底端通过长度可忽略的光滑小圆弧与光滑水平面连接..A、B是两个质量均为 m=1㎏的小滑块(可视为质点),B的左端连有轻质弹簧,处于静止状态.当滑块A置于斜面上且受到大小F=4N,方向垂直斜面向下的恒力作用时,恰能沿斜面向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L=1m处由静止开始下滑,若取g=10m/s2,sinα=0.6,cosα=0.8.求:
如图所示,粗糙斜面其倾角为α,底端通过长度可忽略的光滑小圆弧与光滑水平面连接..A、B是两个质量均为 m=1㎏的小滑块(可视为质点),B的左端连有轻质弹簧,处于静止状态.当滑块A置于斜面上且受到大小F=4N,方向垂直斜面向下的恒力作用时,恰能沿斜面向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L=1m处由静止开始下滑,若取g=10m/s2,sinα=0.6,cosα=0.8.求: