题目内容
【题目】如图所示,a、b两个物体,ma=2mb , 它们与斜面间的动摩擦因素μ相同,用细绳连接后放在倾角为θ的斜面上(μ<tanθ),在它们加速下滑的过程中( )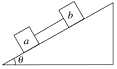
A.细绳有张力,a和b加速度相等,且加速度a<gsinθ
B.细绳无张力,a和b加速度相等,且加速度a<gsinθ
C.细绳的张力大于mgsinθ
D.细绳的张力等于mgsinθ
【答案】B
【解析】解:对a、b组成的整体为研究对象,分析受力可知,整体受重力、弹力、滑动摩擦力.由牛顿第二定律可知:
(ma+mb)gsinθ﹣μ(ma+mb)gcosθ=(ma+mb)a
解得:a=gsinθ﹣μgcosθ<gsinθ;
设细绳的张力为T,对b分析,根据牛顿第二定律得:
mbgsinθ+T﹣μmbgcosθ=mba
解得 T=0,即细绳的张力 T=0;B符合题意,ACD不符合题意;
故答案为:B
先对整体进行研究,根据牛顿第二运动定律,求出整体的加速度。再隔离出a物体根据牛顿第二运动定律判断。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在做“探究加速度和力、质量的关系”的实验中,保持小车和砝码的总质量不变,测得小车的加速度a和拉力F的数据如下表所示
F (N) | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
a (m/s2) | 0.11 | 0.19 | 0.29 | 0.40 | 0.51 |
(1)根据中的数据在坐标图上作出a﹣F图象;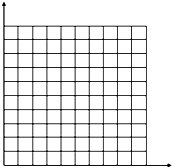
(2)图象斜率的物理意义是;
(3)小车和砝码的总质量为kg;
(4)图线(或延长线)与F轴截距的物理意义是 .