Question

【题目】如图所示，A、B叠放在光滑水平地面上，B 与自由长度为L0的轻弹簧相连，当系统 振动时，A、B始终无相对滑动，已知mA＝3m ， mB＝m ， 当振子距平衡位置的位移x的大小为时，系统的加速度大小为a ， 求：A、B间摩擦力Ff与位移x的函数关系．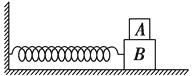

Answer 1

【答案】设弹簧的劲度系数 为k ， 以A、B整体为研究对象，系统在水平方向上做简谐运动，其中弹簧的弹力作为系统的回复力，所以对系统运动到距平衡位置 时，
有 ,
由此得 ①
当系统的位移为x时，A、B间的静摩擦力为 ,此时A、B具有共同加速度 ，对系统有
′②
对A有 ，③
结合①②③式有
【解析】对整体分析，根据牛顿第二定律求出劲度系数，从而通过整体和隔离法得出A、B间的摩擦力与位移x的函数关系。
【考点精析】利用简谐运动对题目进行判断即可得到答案，需要熟知谐运动是一种变加速运动，在平衡位置时，速度最大，加速度为零;在最大位移处，速度为零，加速度最大．