题目内容
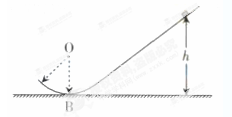
(15分)运动员驾驶摩托车做腾跃特技表演是一种刺激性很强的运动项目．如图所示，AB是水平路面，BC是半径为20m的圆弧，CDE是一段曲面．运动员驾驶功率始终是P＝1.8kW的摩托车在AB段加速，到B点时速度达到最大vm＝20m/s，再经t＝13s的时间通过坡面到达E点时，关闭发动机后水平飞出．已知人和车的总质量m＝180kg，坡顶高度h＝5m，落地点与E点的水平距离s＝16m，重力加速度g＝10m/s2．如果在AB段摩托车所受的阻力恒定，求：
⑴AB段摩托车所受阻力的大小；
⑵摩托车过B点时受到地面支持力的大小；
⑶摩托车在冲上坡顶的过程中克服阻力做的功．
⑴AB段摩托车所受阻力的大小；
⑵摩托车过B点时受到地面支持力的大小；
⑶摩托车在冲上坡顶的过程中克服阻力做的功．
⑴f＝90N；⑵N＝5400N；⑶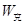
＝27360J。
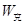＝27360J。试题分析：⑴由于摩托车到B点时速度达到最大，
即到B点时所受牵引力与阻力大小相等，
因此有：f＝F＝
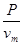
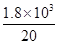N＝90N⑵在B点处，摩托车受重力mg、地面的支持力N作用，
根据牛顿第二定律有：N－mg＝
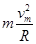
解得：N＝m(g＋
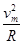)＝180×(10＋
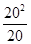)N＝5400N⑶设摩托车从E点开始做平抛运动的速度为v，
根据平抛运动规律有：s＝
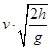，解得：v＝
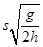
设摩托车在冲上坡顶的过程中阻力做的功为Wf，
根据动能定理有：Pt－mgh＋Wf＝
－
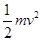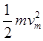
则摩托车在冲上坡顶的过程中克服阻力做的功为：
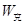＝－Wf联立以上各式并代入数据解得：
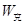＝27360J
练习册系列答案
阅读快车系列答案
相关题目
