题目内容
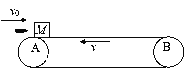
【题目】如图所示,质量为M=1kg的小木块随水平传送带一起以v=2m/s的速度向左匀速运动,传送带两端A、B间距为L=0.8m,小木块与传送带的动摩擦因数μ=0.5。当木块运动到最左端A点时,一颗质量为m=20g的子弹,以v0=300m/s的水平向右的速度射入木块,并在极短的时间内穿出,穿出速度vm=50m/s,重力加速度g取10m/s2。求:
(1)子弹穿出小木块时小木块的速度vM;
(2)子弹射穿小木块过程中产生的热量Q;
(3)小木块在传送带上运动的时间。
【答案】(1)3m/s;(2)872.5J;(3)0.4s
【解析】(1)子弹射过小木块过程,子弹和木块组成的系统动量守恒,根据动量守恒定律求解出子弹穿出小木块时小木块的速度![]() ;(2)子弹射穿小木块过程中产生的热量Q等于系统机械能的损失,根据能量守恒定律求解;(3)根据牛顿第二定律和运动学公式结合求出木块在传送带上速度减到0时的位移,判断小木块从哪端离开传送带,再由位移时间公式求解时间.
;(2)子弹射穿小木块过程中产生的热量Q等于系统机械能的损失,根据能量守恒定律求解;(3)根据牛顿第二定律和运动学公式结合求出木块在传送带上速度减到0时的位移,判断小木块从哪端离开传送带,再由位移时间公式求解时间.
(1)子弹和木块组成的系统动量守恒,以向右为正方向
由动量守恒定律有: ![]()
代入数据解得木块的速度: ![]() ,方向水平向右
,方向水平向右
(2)根据能量守恒定律得:
子弹射穿小木块过程中产生的热量![]()
代入数据解得: ![]()
(3)设木块在传送带上速度减到0时的位移为s
由牛顿第二定律得: ![]()
解得: ![]()
由速度与位移关系式得: ![]()
解得: ![]()
所以木块会在右边离开传送带,设在传送带上的时间为t
则有: ![]()
解得: ![]() (不合题意舍去)
(不合题意舍去)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目