题目内容
如图所示,固定在地面上的光滑轨道AB、CD,均是半径为R的
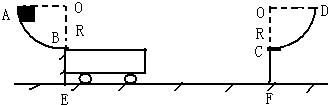
圆弧.一质量为m、上表面长也为R的小车静止在光滑水平面EF上,小车上表面与轨道AB、CD的末端B、C相切.一质量为m的物体(大小不计)从轨道AB的A点由静止下滑,由末端B滑上小车,小车在摩擦力的作用下向右运动.当小车右端与壁CF接触前的瞬间,物体m恰好滑动到小车右端相对于小车静止,同时小车与CF相碰后立即停止运动但不粘连,物体则继续滑上轨道CD.求:
(1)物体滑上轨道CD前的瞬间时速率;
(2)水平面EF的长度;
(3)当物体再从轨道CD滑下并滑上小车后,如果小车与壁BE相碰后速度也立即变为零,最后物体m停在小车上的Q点,则Q点距小车右端多远?
| 1 | 4 |
(1)物体滑上轨道CD前的瞬间时速率;
(2)水平面EF的长度;
(3)当物体再从轨道CD滑下并滑上小车后,如果小车与壁BE相碰后速度也立即变为零,最后物体m停在小车上的Q点,则Q点距小车右端多远?

分析:(1)根据机械能守恒定律求出物体滑动B点是的速度,因为当小车右端与壁CF接触前的瞬间,物体m恰好滑动到小车右端相对于小车静止结合动量守恒定律求出物体滑上轨道CD前的瞬间时速率.
(2)根据能量守恒定律fR=
mvo2-
2mv12求出水平面EF的长度.
(3)物体从CD滑下后与小车达到相对静止,有共同速度,结合动能定理对小车和物体分析,分别求出物体相对小车的位移和小车滑行的位移.从而得出Q点距小车右端的距离.
(2)根据能量守恒定律fR=
| 1 |
| 2 |
| 1 |
| 2 |
(3)物体从CD滑下后与小车达到相对静止,有共同速度,结合动能定理对小车和物体分析,分别求出物体相对小车的位移和小车滑行的位移.从而得出Q点距小车右端的距离.
解答:解:(1)设物体从A滑至B时速率为Vo,根据机械能守恒定律有:mgR=
mvo2
vo=
物体与小车相互作用过程中,系统动量守恒,设共同速度为V1,有:mvo=2mv1
解得物体滑上轨道CD前的瞬间时速率:v1=
(2)设二者之间的摩擦力为f,根据动能定理有,
对物体有:-fSEF=
mv12-
mvo2
对小车有:f(SEF-R)=
mv12
(或对系统根据能量守恒定律有:fR=
mvo2-
2mv12)
得f=
mg
SEF=
R
(3)设物体从CD滑下后与小车达到相对静止,共同速度为V2,相对小车滑行的距离为S1,小车停后物体做匀减速运动,相对小车滑行距离为S2,根据动量守恒和能量守恒有:
mv1=2mv2
fS1=
mv12-
2mv22
对物体根据动能定理有:fS2=
mv22
解得S1=
RS2=
R
则Q点距小车右端距离:S=S1+S2=
R
答:(1)物体滑上轨道CD前的瞬间时速率v1=
.
(2)水平面EF的长度为
R.
(3)最后物体m停在小车上的Q点,则Q点距小车右端
R.
| 1 |
| 2 |
vo=
| 2gR |
物体与小车相互作用过程中,系统动量守恒,设共同速度为V1,有:mvo=2mv1
解得物体滑上轨道CD前的瞬间时速率:v1=
| ||
| 2 |
(2)设二者之间的摩擦力为f,根据动能定理有,
对物体有:-fSEF=
| 1 |
| 2 |
| 1 |
| 2 |
对小车有:f(SEF-R)=
| 1 |
| 2 |
(或对系统根据能量守恒定律有:fR=
| 1 |
| 2 |
| 1 |
| 2 |
得f=
| 1 |
| 2 |
SEF=
| 3 |
| 2 |
(3)设物体从CD滑下后与小车达到相对静止,共同速度为V2,相对小车滑行的距离为S1,小车停后物体做匀减速运动,相对小车滑行距离为S2,根据动量守恒和能量守恒有:
mv1=2mv2
fS1=
| 1 |
| 2 |
| 1 |
| 2 |
对物体根据动能定理有:fS2=
| 1 |
| 2 |
解得S1=
| 1 |
| 4 |
| 1 |
| 8 |
则Q点距小车右端距离:S=S1+S2=
| 3 |
| 8 |
答:(1)物体滑上轨道CD前的瞬间时速率v1=
| ||
| 2 |
(2)水平面EF的长度为
| 3 |
| 2 |
(3)最后物体m停在小车上的Q点,则Q点距小车右端
| 3 |
| 8 |
点评:本题综合考查了动能定理、机械能守恒定律以及能量守恒定律,关键是理清运动的规程,选择合适的规律进行求解.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
如图所示,固定在地面上的光滑斜面顶端固定一弹簧.一物体向右滑行,冲上斜面并压缩弹簧.设物体通过斜面最低点A时的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则弹簧被压缩至最短时具有的弹性势能为

|
C.-mgh D.-(mgh+mv2)
 如图所示,固定在地面上的光滑斜面顶端固定一弹簧.一物体向右滑行,冲上斜面并压缩弹簧.设物体通过斜面最低点A时的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则弹簧被压缩至最短时具有的弹性势能为 ( )
如图所示,固定在地面上的光滑斜面顶端固定一弹簧.一物体向右滑行,冲上斜面并压缩弹簧.设物体通过斜面最低点A时的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则弹簧被压缩至最短时具有的弹性势能为 ( ) 如图所示,固定在匀强磁场中的水平导轨ab、cd的间距L1=0.5m,金属棒ad与导轨左端bc的距离L2=0.8m,整个闭合回路的电阻为R=0.2Ω,匀强磁场的方向竖直向下穿过整个回路.ad杆通过细绳跨过定滑轮接一个质量m=0.04kg的物体,不计一切摩擦.现使磁感应强度从零开始以
如图所示,固定在匀强磁场中的水平导轨ab、cd的间距L1=0.5m,金属棒ad与导轨左端bc的距离L2=0.8m,整个闭合回路的电阻为R=0.2Ω,匀强磁场的方向竖直向下穿过整个回路.ad杆通过细绳跨过定滑轮接一个质量m=0.04kg的物体,不计一切摩擦.现使磁感应强度从零开始以
