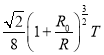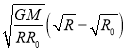题目内容
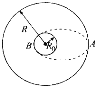
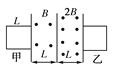
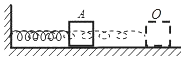
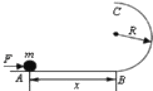
【题目】如图所示,光滑水平面AB=x,其右端B处连接一个半径为R的竖直光滑半圆轨道,C为最高点.质量为m可视为质点的小物块静止在A处,若用水平恒力将小物块推到B处后撤去该水平恒力,重力加速度为g,求:
(1)如果小物块能够通过半圆轨道的最高点C,水平恒力对小物块做的最小功为多少;
(2)如果小物块沿半圆轨道运动到C处后恰好抛落到A处,则X取何值时,在整个运动过程中,水平恒力F最小?最小值为多少?
【答案】(1)![]() (2)当X=4R时,力F有最小值,最小力F=mg.
(2)当X=4R时,力F有最小值,最小力F=mg.
【解析】(1)做功最小时vC应该取最小值,即小物块恰好通过C点,小物块恰好通过C点时,只有重力提供圆周运动向心力,由牛顿定律有:mg=m![]() … ①
… ①
由能量守恒定律有: ![]() ②
②
联立①②解得: ![]()
(2)质点做平抛运动回到A点,设质点经过C点时速度为vC,由平抛运动规律有:
小球在水平方向做匀速直线运动:x=vCt ③
小球在竖直方向做自由落体运动:2R=![]() gt2 ④
gt2 ④
A到C过程只有推力F和重力对物体做功,由动能定理有:
FX﹣2mgR=![]() mvC2 ⑤
mvC2 ⑤
联立③④⑤解得: 解得:F=![]() ⑥
⑥
由⑥可得,当X=4R时,力F有最小值,最小力F=mg.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目