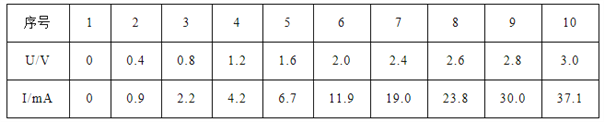
题目内容
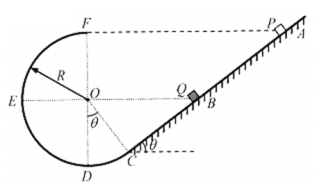
【题目】如图,倾角θ=370的直轨道AC与光滑圆弧轨道CDEF在C处平滑连接,整个装置固定在同一竖直平面内。圆弧轨道的半径为R,DF是竖直直径,以O为圆心,E、O、B三点在同一水平线上,A、F也在同一水平线上。两个小滑块P、Q(都可视为质点)的质量都为m。已知滑块Q与轨道AC间存在摩擦力且动摩擦因数处处相等,而滑块P与直轨道AC的摩擦不计。开始时滑块Q静止于B处,之后让P由静止从A处释放,在B点与Q相碰,碰后P、Q立刻一起向下且在BC段保持匀速运动。已知P、Q每次相碰都会立刻合在一起运动但两者并不粘连,sin370=0.6,cos370=0.8,取重力加速度为g,求:
(1)两滑块进入圆弧轨道运动过程中对圆弧轨道的压力的最大值。
(2)滑块Q在轨道AC往复运动经过的最大路程。
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1) 滑块P下滑至碰前,由机械能守恒定律得
![]()
P、Q碰后一起运动,由动量守恒定律得
mv1=2mv2
P、Q一起运动至D点过程,有
![]()
经过D点时对圆弧轨道的压力最大,有
ND-2mg=2m![]()
由牛顿第三定律可知,两滑块对圆弧轨道最大压力
ND′= ND
解得:
ND′=3.8mg
(2) 由以上计算可知,P、Q整体在D点的动能
![]()
因此它们在圆弧轨道上运动的最高点在E点下方,之后沿轨道返回,再次到达C点的速度大小仍为v2.从C点上滑后P、Q分离,Q比P先到达最高点,且Q运动到最高点时停下。设P、Q上滑的最大位移分别为xP、xQ.对P、Q,由动能定理分别可得
mgsinθxp=![]()
(mgsinθ+f)xQ=![]()
由前面P、Q一起匀速下滑可知Q所受的滑动摩擦力
f=2mgsinθ
P再次从最高点下滑至第二次碰Q前,有
mgsinθ(xP-xQ)=![]()
P、Q碰后一起运动,有
mv3=2mv4
在P、Q第二次进入直轨道AC运动全过程,Q克服摩擦力做的功
Wf=f2xQ
而P、Q碰撞损失的机械能为
![]()
由以上各式可以解得Q克服摩擦力做的功与P、Q碰撞损失的机械能之比
![]()
P、Q此后多次进入直轨道AC运动过程,遵循同样的规律,直到最后到达C点的速度减为0,因此从P、Q第二次进入直轨道AC运动到最后不再进入为止,Q克服摩擦力做的功为
![]()
滑块Q在轨道AC上往复运动经过的最大路程
lm=l+![]()
由以上各式解得
lm=![]()

 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案