题目内容
质量为m=2.0kg的物体,静止在长L=6.0m、距地面高为H=5.0m的平台上的一端,用大小为F=12N的水平推力使物体向平台的另一端做匀加速直线运动,已知物体与平台间的动摩擦因数为μ=0.30.求:
(1)物体受到平台的摩擦力大小;
(2)物体在平台上运动时加速度的大小;
(3)当物体运动到平台另一端时,撤去力F的作用,物体落地时的动能.
(1)物体受到平台的摩擦力大小;
(2)物体在平台上运动时加速度的大小;
(3)当物体运动到平台另一端时,撤去力F的作用,物体落地时的动能.
分析:(1)由共点力的平衡条件可求得物体受到的摩擦力;
(2)由牛顿第二定律可求得加速度大小;
(3)撤去拉力后,物体在空中做平抛运动,由机械能守恒可求得落地时的动能.
(2)由牛顿第二定律可求得加速度大小;
(3)撤去拉力后,物体在空中做平抛运动,由机械能守恒可求得落地时的动能.
解答:解:(1)由于物体在竖直方向合力为0,故:物体受到的摩擦力的大小F1=μFN=μmg=6N;
(2)根据牛顿第二定律F合=ma
物体加速度的大小a=
=3 m/s2
(3)当物体运动到平台另一端时,撤去力F的作用,物体被抛出.
此时物体的速度为v1,有:v12=2aL=36(m/s)2
以地面为势能零点,由于只有重力做功,所以机械能守恒
有:mgH+
mv12=
mv22
解出物体落地时的动能:EK2=
mv22=136J
答:(1)摩擦力大小为6N;(2)加速度大小为3m/s2;(3)落地时的动能为136J.
(2)根据牛顿第二定律F合=ma
物体加速度的大小a=
| F-F1 |
| m |
(3)当物体运动到平台另一端时,撤去力F的作用,物体被抛出.
此时物体的速度为v1,有:v12=2aL=36(m/s)2
以地面为势能零点,由于只有重力做功,所以机械能守恒
有:mgH+
| 1 |
| 2 |
| 1 |
| 2 |
解出物体落地时的动能:EK2=
| 1 |
| 2 |
答:(1)摩擦力大小为6N;(2)加速度大小为3m/s2;(3)落地时的动能为136J.
点评:本题中物体经历了三个过程,分别为匀速直线运动、匀加速直线运动及平抛运动,要合理地选用物理规律分段求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
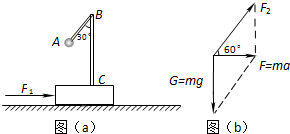 如图(a)所示,质量M=10.0kg的滑块放在水平地面上,滑块上固定一个轻细杆ABC,∠ABC=30°.在A端固定一个质量为m=2.0kg的小球,滑块与地面间的动摩擦因数μ=0.50.现对滑块施加一个水平向右的推力F1=180N,使滑块做匀加速运动.求此时轻杆对小球作用力F2的大小和方向.(取g=10m/s2)
如图(a)所示,质量M=10.0kg的滑块放在水平地面上,滑块上固定一个轻细杆ABC,∠ABC=30°.在A端固定一个质量为m=2.0kg的小球,滑块与地面间的动摩擦因数μ=0.50.现对滑块施加一个水平向右的推力F1=180N,使滑块做匀加速运动.求此时轻杆对小球作用力F2的大小和方向.(取g=10m/s2) (2007?南通模拟)如图所示,水平面上的轻弹簧一端与物体相连,另一端固定在墙上P点,已知物体的质量为m=2.0kg,物体与水平面间的动摩擦因数μ=0.4,弹簧的劲度系数k=200N/m.现用力F拉物体,使弹簧从处于自然状态的O点由静止开始向左移动10cm,这时弹簧具有弹性势能EP=1.0J,物体处于静止状态.若取g=10m/s2,则撤去外力F后( )
(2007?南通模拟)如图所示,水平面上的轻弹簧一端与物体相连,另一端固定在墙上P点,已知物体的质量为m=2.0kg,物体与水平面间的动摩擦因数μ=0.4,弹簧的劲度系数k=200N/m.现用力F拉物体,使弹簧从处于自然状态的O点由静止开始向左移动10cm,这时弹簧具有弹性势能EP=1.0J,物体处于静止状态.若取g=10m/s2,则撤去外力F后( ) 的变化关系如图2所示(图象前3s内为二次函数,3-4.5s内为一次函数,取向左运动的方向为正方向).已知传送带的速度保持不变,g取10m/s2,求:
的变化关系如图2所示(图象前3s内为二次函数,3-4.5s内为一次函数,取向左运动的方向为正方向).已知传送带的速度保持不变,g取10m/s2,求: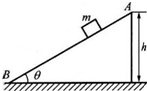 如图所示,质量为m=2.0kg的小滑块,由静止开始从倾角θ=37°的固定的光滑斜面的顶端A滑至底端B,A点距离水平地面的高度h=5.0m,重力加速度g取10m/s2,(sin37°=0.6,cos37°=0.8),试分析:
如图所示,质量为m=2.0kg的小滑块,由静止开始从倾角θ=37°的固定的光滑斜面的顶端A滑至底端B,A点距离水平地面的高度h=5.0m,重力加速度g取10m/s2,(sin37°=0.6,cos37°=0.8),试分析: 如图所示,轻绳悬挂一质量为m=2.0kg的小球,现对小球再施加一个力F,使小球静止在绳子与竖直方向成60°的位置上,g取10m/s2.
如图所示,轻绳悬挂一质量为m=2.0kg的小球,现对小球再施加一个力F,使小球静止在绳子与竖直方向成60°的位置上,g取10m/s2.