题目内容
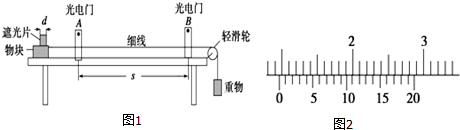
11.如图1所示为测量物块与水平桌面之间动摩擦因数的实验装置图.实验步骤如下:①用天平测量物块和遮光片的总质量M,重物的质量m,用游标卡尺测量遮光片的宽度d,用米尺测量两光电门之间的距离s;
②调整轻滑轮,使细线水平;
③让物块从光电门A的左侧由静止释放,用数字毫秒计分别测出遮光片经过光电门A和光电门B所用的时间△tA和△tB,求出加速度a;
④多次重复步骤③,求a的平均值$\overline{a}$;
⑤根据上述实验数据求出动摩擦因数μ.
回答下列问题:
(1)下列说法正确的是C
A.此实验需要平衡摩擦力
B.此实验需要满足条件:M远大于m
C.此实验需要遮光片的宽度d尽量小些
D.此实验需要两光电门之间的距离s尽量小些
(2)测量d时,某次游标卡尺(主尺的最小分度为1mm)如图2所示.其读数为9.60 mm.
(3)物块的加速度a可用d、s、△tA和△tB表示为a=$\frac{1}{2s}[{{{({\frac{d}{{△{t_B}}}})}^2}-{{({\frac{d}{{△{t_A}}}})}^2}}]$.
(4)动摩擦因数μ可用M、m、$\overline{a}$和重力加速度g表示为μ=$\frac{{mg-({M+m})\overline a}}{Mg}$.
(5)如果细线没有调整到水平,由此引起的误差属于系统误差(填“偶然误差”或“系统误差”).
分析 (1)根据实验的目的和要求事项分析答题;
(2)游标卡尺主尺与游标尺的示数之和是游标卡尺的示数;
(3)由速度公式求出物块经过A、B两点时的速度,然后由匀变速运动的速度位移公式求出物块的加速度;
(4)由牛顿第二定律求出动摩擦因数.
(5)由于实验设计造成的误差是系统误差,由于实验操作、读数等造成的误差属于偶然误差.
解答 解:(1)A、该实验的目的是为了测量物块与长木板之间的摩擦因数,所以在实验的过程中,不能调整长木板倾斜程度,平衡摩擦力,否则不能测量摩擦因数.故A错误.
B、实验原理中,可以以整体为研究对象,求出加速度的表达式,所以不需要满足M远大于m.故B错误;
C、由于在测量A、B两点的速度时,使用平均速度来代替瞬时速度,所以d小一些误差会更小.故C正确;
D、在数据处理中,使用速度位移公式得:vB2-vA2=2as:所以两光电门之间的距离s太小可能会增大实验的误差.故D错误.
故选:C.
(2)由图(b)所示游标卡尺可知,主尺示数为9mm,游标尺示数为12×0.05mm=0.60mm,则游标卡尺示数为9mm+0.600mm=9.60mm.
(3)物块经过A点时的速度vA=$\frac{d}{{t}_{A}}$,物块经过B点时的速度vB=$\frac{d}{{t}_{B}}$,物块做匀变速直线运动,由速度位移公式得:vB2-vA2=2as,加速度a=$\frac{1}{2s}[{{{({\frac{d}{{△{t_B}}}})}^2}-{{({\frac{d}{{△{t_A}}}})}^2}}]$;
(4)以M、m组成的系统为研究对象,由牛顿第二定律得:mg-μMg=(M+m)$\overline{a}$,解得μ=$\frac{{mg-({M+m})\overline a}}{Mg}$;
(5)如果细线没有调整到水平,由此引起的误差属于系统误差.
故答案为:(1)C;(2)9.60;(3)$\frac{1}{2s}[{{{({\frac{d}{{△{t_B}}}})}^2}-{{({\frac{d}{{△{t_A}}}})}^2}}]$;(4)$\frac{{mg-({M+m})\overline a}}{Mg}$;(5)系统误差.
点评 对游标卡尺进行读数时,要先确定游标尺的精度,主尺与游标尺的示数之和是游标卡尺示数,读数时视线要与刻度线垂直.

 特高级教师点拨系列答案
特高级教师点拨系列答案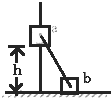 如图,滑块a、b的质量均为m,a套在固定直杆上,与光滑水平地面相距h,b放在地面上,a、b通过铰链用刚性轻杆连接.不计摩擦,a、b可视为质点,重力加速度大小为g.则( )
如图,滑块a、b的质量均为m,a套在固定直杆上,与光滑水平地面相距h,b放在地面上,a、b通过铰链用刚性轻杆连接.不计摩擦,a、b可视为质点,重力加速度大小为g.则( )| A. | a落地前,轻杆对b一直做正功 | |
| B. | a落地时速度大小为$\sqrt{2gh}$ | |
| C. | a下落过程中,其加速度大小始终不大于g | |
| D. | a落地前,当a的机械能最小时,b对地面的压力大小为mg |
 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )| A. | 环到达B处时,重物上升的高度$h=\frac{d}{2}$ | |
| B. | 环到达B处时,环与重物的速度大小相等 | |
| C. | 环从A处释放时,环的加速度为g | |
| D. | 环从A到B,环减少的机械能等于重物增加的机械能 |
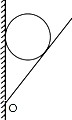 如图所示,光滑小球置于竖直墙壁和挡板间,挡板绕O点于图示位置缓慢转至水平的 过程中,球对墙壁和挡板的压力如何变化( )
如图所示,光滑小球置于竖直墙壁和挡板间,挡板绕O点于图示位置缓慢转至水平的 过程中,球对墙壁和挡板的压力如何变化( )| A. | 对墙壁的压力减小,对挡板的压力也减小 | |
| B. | 对墙壁的压力减小,对挡板的压力增大 | |
| C. | 对墙壁的压力减小,对挡板的压力先增大后减小 | |
| D. | 对墙壁的压力先增大后减小,对挡板的压力增大 |
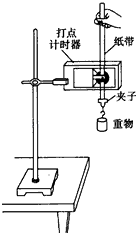 如图所示,打点计时器固定在铁架台上,使重物带动纸带从静止开始自由下落,利用此装置可以测重力加速度.所需器材有电磁打点计时器(带导线),纸带和复写纸以及带铁夹的铁架台.重锤,除此之外还需要的实验器材有:刻度尺.6V交流电(学生电源).
如图所示,打点计时器固定在铁架台上,使重物带动纸带从静止开始自由下落,利用此装置可以测重力加速度.所需器材有电磁打点计时器(带导线),纸带和复写纸以及带铁夹的铁架台.重锤,除此之外还需要的实验器材有:刻度尺.6V交流电(学生电源). 如图所示,匀强电场中有a、b、c三点,ab与场强方向平行,bc与场强方向成60°,ab=4cm,bc=8cm,将一个带电量为2×10-8C的电荷从a移到b时,电场力做功4×10-8J.求:
如图所示,匀强电场中有a、b、c三点,ab与场强方向平行,bc与场强方向成60°,ab=4cm,bc=8cm,将一个带电量为2×10-8C的电荷从a移到b时,电场力做功4×10-8J.求: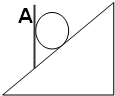 如图所示,斜面倾角θ=30°,光滑小球所受的重力为20N,在竖直挡板AB的作用下,小球静止在斜面上,小球对挡板和斜面的压力大小分别是多少?
如图所示,斜面倾角θ=30°,光滑小球所受的重力为20N,在竖直挡板AB的作用下,小球静止在斜面上,小球对挡板和斜面的压力大小分别是多少?