题目内容
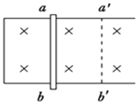
如图所示,在倾角为口的光滑斜面上,存在着两个磁感应强度大小均为B的匀强磁场,区域Ⅰ磁场方向垂直斜面向下,区域Ⅱ磁场方向垂直斜面向上,磁场宽度均为L,一个质量为m,电阻为R,边长也为L的正方形线框,由静止开始下滑,沿斜面滑行一段距离后ab边刚越过ee′进入磁场区域时,恰好做匀速直线运动,若当ab边到达gg′与ff′的中间位置时,线框又恰好做匀速直线运动.求:
(1)当ab边到达gg′与ff′的中间位置时做匀速直线运动的速度v.
(2)当ab边刚越过ff′进入磁场区域Ⅱ时,线框的加速度a.
(3)线框从ab边开始进入磁场Ⅰ至ab边到达gg′与ff′的中间位置的过程中产生的热量Q.

(1)当ab边到达gg′与ff′的中间位置时做匀速直线运动的速度v.
(2)当ab边刚越过ff′进入磁场区域Ⅱ时,线框的加速度a.
(3)线框从ab边开始进入磁场Ⅰ至ab边到达gg′与ff′的中间位置的过程中产生的热量Q.

(1)正方形线框的ab边刚越过ee′线后即作匀速运动,设速度为v′.则有
mgsinθ=BIL,
又I=
,则得:mgsinθ=
,①
当ab边到达gg′与ff′的中间位置时,线框又做匀速运动,则有:
E=2BLv,I′=
根据平衡条件得:mgsinθ=2BI′L
联立得:mgsinθ=
解得:v=
②
(2)当ab边刚越过ff′进入磁场区域Ⅱ时,根据牛顿第二定律得:
2B
L-mgsinθ=ma ③
由①③得:a=3gsinθ
(3)由能量关系可求得:
Q=mg?
Lsinθ+
mv′2-
mv2=
mgLsinθ+
答:(1)当ab边到达gg′与ff′的中间位置时做匀速直线运动的速度v为
.
(2)当ab边刚越过ff′进入磁场区域Ⅱ时,线框的加速度a为3gsinθ.
(3)线框从ab边开始进入磁场Ⅰ至ab边到达gg′与ff′的中间位置的过程中产生的热量Q为
mgLsinθ+
.
mgsinθ=BIL,
又I=
| BLv′ |
| R |
| B2L2v′ |
| R |
当ab边到达gg′与ff′的中间位置时,线框又做匀速运动,则有:
E=2BLv,I′=
| E |
| R |
根据平衡条件得:mgsinθ=2BI′L
联立得:mgsinθ=
| 4B2L2v |
| R |
解得:v=
| mgRsinθ |
| 4B2L2 |
(2)当ab边刚越过ff′进入磁场区域Ⅱ时,根据牛顿第二定律得:
2B
| 2BLv′ |
| R |
由①③得:a=3gsinθ
(3)由能量关系可求得:
Q=mg?
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 15m3g2R2sin2θ |
| 32B4L4 |
答:(1)当ab边到达gg′与ff′的中间位置时做匀速直线运动的速度v为
| mgRsinθ |
| 4B2L2 |
(2)当ab边刚越过ff′进入磁场区域Ⅱ时,线框的加速度a为3gsinθ.
(3)线框从ab边开始进入磁场Ⅰ至ab边到达gg′与ff′的中间位置的过程中产生的热量Q为
| 3 |
| 2 |
| 15m3g2R2sin2θ |
| 32B4L4 |

练习册系列答案
相关题目