Question

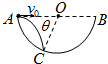
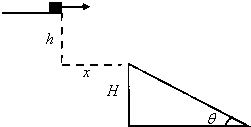
一可看作质点滑块从一平台右端以某一速度水平抛出，恰好到右下方倾角为θ=30⁰的斜面顶端时速度沿斜面方向并沿斜面运动到斜面底端．已知平台到斜面顶端的竖直高度h=1.25m，斜面与滑块之间的摩擦因数为μ=

3

5

，斜面顶端底端的竖直高度H=100m，g=10m/s²求：
（1）滑块水平抛出的初速度大小v₀
（2）滑块从抛出到斜面底端的时间t．

Answer 1

（1）设从抛出到达斜面顶端的时间为t₁，此时竖直方向的速度为v_y，则由运动学公式得：

1

2

g

t

21

=h，v_y=gt₁，
解得：t₁=0.5s，v_y=5m/s
因为达到斜面顶端的速度方向沿斜面向下，所以有：
tanθ=

vy

v0

解得：v₀=

vy

tanθ

=

5

3 3

m/s=5

3

m/s
（2）设达到斜面顶端速度为v′，从斜面顶端到斜面底端的加速度为a，时间为t₂，
则 v′=

vy

sin30°

=2v_y=10m/s
根据牛顿第二定律得：mgsinθ-μmgcosθ=ma，
则得 a=g（sinθ-μcosθ）=10×（sin30°-

3

5

×cos30°）=2m/s²；
由v′t₂+

1

2

a

t

22

=

H

sinθ

得：
10t₂+

1

2

×2×

t

22

=

100

sin30°

解得：t₂=10s，t₂=-20s（舍去）
所以总时间t=t₁+t₂=0.5s+10s=10.5s
答：
（1）滑块水平抛出的初速度大小v₀为5

3

m/s．
（2）滑块从抛出到斜面底端的时间t为10.5s．