题目内容

如图所示，在竖直平面内有一半圆形轨道，圆心为O，一质点小球从与圆心等高的圆形轨道上的A点以速度v0水平向右抛出，落于圆轨道上的C点，已知OC的连线与OA的夹角为θ，求小球从A到C的时间t=？（空气阻力不计）
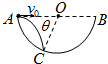
由几何关系可知，AC水平方向的夹角为α=
π-θ
2
．根据抛体运动的规律，
知tanα=
y
x
=
1
2
gt2
v0t
=
gt
2v0

则t=
2v0tanα
g
=
2v0
g
cot
θ
2
．
答：小球从A到C的时间为
2v0
g
cot
θ
2
．
练习册系列答案
相关题目
将一物体从空间某处水平抛出，在落地前1S内，它的速度与水平方向的夹角由30°变为60°，g取10m/s2不计空气阻力的影响，则下列说法不正确的（　　）
A．平抛运动的初速度为5
3
m/s
B．从抛出经1.5s落地
C．落地前1s内速度的变化量大小为10m/s，方向与落地时速度方向同向
D．物体是从11.25m处下落的
从离地面高为5m处以10m/s的初速度水平抛出一物体，若不计空气阻力，g取10m/s2，则（　　）
A．物体从抛出到落地的时间为1s
B．物体落地时在竖直方向的分速度为20m/s
C．物体抛出点到落地点的水平距离是10m
D．物体落地时的位移是15m
在同一竖直线上A、B两点向同一方向水平抛物，A的高度为H，抛出的物体水平位移为2S，B的高度为2H，抛出的物体水平位移为S，两轨迹通过同一点C，求C点的高度．
下列关于平抛运动及两个分运动的说法正确的是（　　）
A．某段时间内的合位移等于两分位移的矢量和，某一时刻的合速度等于两分速度的矢量和
B．两个分运动是先后进行的
C．水平方向速度大小并不影响物体竖直方向的运动
D．两个分运动和合运动在时间上是相等的
如图所示，一可视为质点的物体质量为m=1kg，在左侧平台上水平抛出，恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道，并沿轨道下滑，A、B为圆弧两端点，其连线水平，O为轨道的最低点．已知圆弧半径为R=1.0m，对应圆心角为θ=106°，平台与AB连线的高度差为h=0.8m．（重力加速度g=10m/s2，sin53°=0.8，cos53°=0.6）求：
（1）物体平抛的初速度；
（2）物体运动到圆弧轨道最低点O时对轨道的压力．
一物体水平抛出，在落地前的最后1秒内，其速度方向由跟水平方向成30°角变为跟水平方向成45°角，求物体抛出时的初速度大小与抛出点离地高度？（不计阻力，g取10m/s2）
如图，轰炸机沿水平方向匀速飞行，到达山坡底端正上方时释放一颗炸弹，并垂直击中山坡上的目标A．已知A点高度为h，山坡倾角为θ，由此可算出（　　）
A．轰炸机的飞行高度B．轰炸机的飞行速度
C．炸弹的飞行时间D．炸弹投出时的动能
一可看作质点滑块从一平台右端以某一速度水平抛出，恰好到右下方倾角为θ=300的斜面顶端时速度沿斜面方向并沿斜面运动到斜面底端．已知平台到斜面顶端的竖直高度h=1.25m，斜面与滑块之间的摩擦因数为μ=
3
5
，斜面顶端底端的竖直高度H=100m，g=10m/s2求：
（1）滑块水平抛出的初速度大小v0
（2）滑块从抛出到斜面底端的时间t．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网