Question

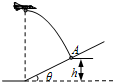
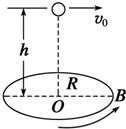
如图所示，半径为R的圆盘匀速转动，在距半径高度h处以平行OB方向水平抛出一小球，抛出瞬间小球的初速度与OB方向平行，为使小球和圆盘只碰撞一次且落点为B，求：
（1）小球的初速度大小；
（2）圆盘转动的角速度．

Answer 1

（1）设小球在空中的飞行时间为t₁，初速度为v₀，圆盘的角速度为ω，
由h=

1

2

gt2得：
小球平抛时间t₁=

2h g

小球水平方向分运动R=v₀t₁
可得v₀=

R

t1

=R

g 2h

（2）当OB再次与v₀平行时，圆盘运动时间t₂=nT（n=1，2，3，4，…），
T=

2π

ω

，
依题意t₁=t₂．
得：

2h g

=

2nπ

ω

，
解得ω=nπ（n=1，2，3，4，…）
答：（1）小球的初速度大小为R

g 2h

．
（2）圆盘转动的角速度为ω=nπ （n=1，2，3，4，…）