题目内容
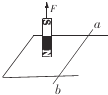
【题目】如图所示，在水平向右的匀强电场中，有一质量为m、带正电的小球，用长为l的绝缘细线悬挂于O点，当小球静止时细线与竖直方向的夹角为θ.现给小球一个初速度，使小球恰能在竖直平面内做圆周运动，试问：
（1）小球在做圆周运动的过程中，在哪一位置速度最小？速度最小值为多少？
（2）小球的初速度应为多大？
【答案】（1）当小球运动至位于与A点对应的同一直径上的另一端点B时，速度最小， 
（2）
【解析】（1）重力与电场力的合力： 
，电场力为：F电=mgtanθ，小球恰好做圆周运动，在平衡位置的反方向上的圆周位置上B点时速度最小，由牛顿第二定律得： 
，
解得小球的最小速度为： 
；
（2）由动能定理可得：-mg2lcosθ-mgtanθ×2lsinθ=
mv2-
mvA2，
解得： 
．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
