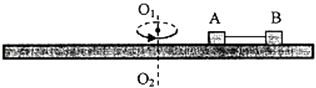
��Ŀ����
����Ŀ�����õ��ɵ���ʹ��ʹ�����װ�ÿ��Խ������������ߴ�����ͼ��ʾ����֪�����ƽ����ˮƽ�����37��ǣ����Ҳ��37��Ĺ⻬б�����̶��ڵ������봫������öԽӣ������¶˹̶���б��ˣ�������Ƥ����Ķ�Ħ��������=0.25�����ʹ�����װ��˳ʱ������ת�����ٶ�v=4m/s�������������L=5m��B��C �ֱ��Ǵ��ʹ������ֵ��е㣬��Ե�봫�ʹ�֮�䲻���ֽ�����m=1kg�Ĺ������ڵ����ϣ�����������ѹ����A ����ɾ�ֹ�ͷţ������뿪б�涥�˻������ʹ��ϵ�B��ʱ�ٶ�v0=8m/s��AB ��ľ���s=1m����������Ϊ�ʵ㣬g ȡ10m/s2��sin37��=0.6��cos37��=0.8������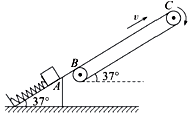
��1�����ɵ���������ܣ�
��2�������ش��ʹ��ϻ���ʱ�䣻
��3������Ƥ���ϻ�����ȫ�������������������Ƕ��٣�
���𰸡�
��1���⣺�����A��B���̣����ɵĵ������ܵļ�С���ڻ����е�ܵ����ӣ����ݻ�е���غ㶨�ɣ��ã�
���ɵ����������Ϊ��Ep=mgssin37��+ ![]() mv02
mv02
�������ݽ�ã�EP=38J��
�𣺵��ɵ������������38J��
��2���⣺�����ش�����������ϻ����Ĺ������У�mgsin37��+��mgcos37��=ma1
�������ݽ�� a1=8m/s2��
��B���˶����봫�ʹ�������Ҫ��ʱ��Ϊ��t1= ![]() =
= ![]() s=0.5s��
s=0.5s��
�������е�λ�ƴ�СΪ��s1= ![]() t1=
t1= ![]() ��0.5m=3m��L��
��0.5m=3m��L��
��Ϊ�̣�tan37�㣬���Թ������ش��ʹ����������ϻ����У�
mgsin37�㩁��mgcos37��=ma2
�������ݽ�ã�a2=4m/s2��
���蹤���ٶȼ�Ϊ��ʱ������δ�Ӵ��ʹ��ϻ��䣬���У�t2= ![]() =
= ![]() s=1s��
s=1s��
�������е�λ�ƴ�СΪ��s2= ![]() t2=
t2= ![]() ��1=2m=L��s1��
��1=2m=L��s1��
�ʼ�������������ش��ʹ��ϻ���ʱ��Ϊ��t=t1+t2=1.5s��
�𣺹����ش��ʹ��ϻ���ʱ��Ϊ1.5s��
��3���⣺������Ƥ�����Լ��ٶ�a1�����Ĺ�����Ƥ����λ��Ϊ
xƤ1=vt1=4��0.5m=2m
������Ƥ��������λ�ƴ�СΪ��x1=s1��xƤ1=3m��2m=1m
������Ƥ�����Լ��ٶ�a2�����Ĺ�����Ƥ����λ��Ϊ
xƤ2=vt2=4��1m=4m
������Ƥ��������λ�ƴ�СΪ��x2=xƤ2��s2=4m��2m=2m
����ȫ�����в����������� Q=��mgcos37�㣨��x1+��x2��
�������ݽ�� Q=6J
�𣺹�����Ƥ���ϻ�����ȫ��������������������6J��
����������1�����ݹ����뿪б�涥�˻���Ƥ���ϵ�B��ʱ�ٶ�v0=8m/s��A��B��ľ���s=lm��ͨ�������غ㶨��������ɵ���������ܣ���2����Ϊ�̣�tan37�㣬�������ٶȼ�Ϊ���ʹ��ٶ�ʱ�����Բ�ͬ�ļ��ٶ����ϼ��٣�����ţ�ٵڶ�������������ȼ���ֱ���˶��ļ��ٶȣ�Ȼ������˶�ѧ��ʽ����ϻ�����ʱ�䣮��3�������˶�ѧ��ʽ���������Ƥ�������Ի�����·�̣����ɻ���Ħ���������·�̵ij˻�����������ܣ�
�����㾫�������ڱ��⿼��ĵ������ܺ��ܹ�ϵ����Ҫ�˽ⵯ���������������ڷ��������α�����е���������ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1���ܵó���ȷ�𰸣�

����Ŀ��Ϊ��֤���ܶ�����ijͬѧ���������ʵ�飮��һ��ֱľ��һ�˵�����һ�˲���װһ�ٶȴ���������С�����ɾ�ֹ��ľ��h�ߴ����Ӵ���������ƽ���������ɻ������ٶȴ�����ʱ���������龭�˴�ʱ���ٶ�v����ͼ��ʾ����θı们����»��߶�h��б�����Dz��䣩����Ӧ���ٶ�ֵ��¼�ڱ��У�
�»��߶�h/m | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
�ٶ�v/ms��1 | 0.633 | 0.895 | 1.100 | 1.265 | 1.414 |
Ҫ���ֱ�۵�˵���˹��̶��ܶ����Ƿ��������ͬѧ��������hΪ���������ϵ������Ϊ����ϵ�ĺ���Ӧ���� �� ��ʵ���Ƿ���Ҫƽ��Ħ��������ǡ�����