题目内容
15. 如图所示,一光滑的半径为R的半圆形竖直轨道AB固定在水平面上.一个质量为m的小球以某一速度冲上轨道,然后小球从轨道口B处水平飞出,最后落在水平面上,已知小球落地点C距B处的水平距离为3R.求:
如图所示,一光滑的半径为R的半圆形竖直轨道AB固定在水平面上.一个质量为m的小球以某一速度冲上轨道,然后小球从轨道口B处水平飞出,最后落在水平面上,已知小球落地点C距B处的水平距离为3R.求:(1)小球在轨道口B处的速度;
(2)小球到A点时对半圆轨道的压力.
分析 (1)小球由B到C做平抛运动,由平抛运动规律可求得小球在B点的速度;
(2)根据机械能守恒可求得小球在A点的速度;再由向心力公式可求得A点小球受到的支持力;由牛顿第三定律可求得压力.
解答 解:(1)小球从B到C作平抛运动;
水平方向3R=vxt;
竖直方向2R=$\frac{1}{2}$gt2;
解得:v=$\frac{3}{2}\sqrt{gR}$;
(2)小球从A到到B点,由机械能守恒得:
$\frac{1}{2}$mvA2=mg•2R+$\frac{1}{2}$MVB2;
小球在A点,由牛顿第二定律可得:
N-mg=m$\frac{{v}_{A}^{2}}{R}$
解得N=$\frac{29}{4}$mg;
由牛顿第三定律可得:小球对半圆轨道的压力为:$\frac{29}{4}$mg;
答:(1)小球在轨道口B处的速度为
(2)小球到A点时对半圆轨道的压力为$\frac{29}{4}$mg;.
点评 解答此题关键是分析小球的运动过程,明确小球分别在B、A的受力,选用牛顿第二定律求解,A到B的过程机械能守恒,B到C的过程做平抛运动.

练习册系列答案
相关题目
6. 如图,平行金属板A、B水平正对放置,分别带等量异种电荷,一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( )
如图,平行金属板A、B水平正对放置,分别带等量异种电荷,一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( )
 如图,平行金属板A、B水平正对放置,分别带等量异种电荷,一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( )
如图,平行金属板A、B水平正对放置,分别带等量异种电荷,一带电微粒水平射入板间,在重力和电场力共同作用下运动,轨迹如图中虚线所示,那么( )| A. | 若微粒带正电,微粒从P到Q电场力一定做正功 | |
| B. | 若微粒带负电,微粒从P到Q电场力一定做正功 | |
| C. | 微粒从P运动到Q动能一定增加 | |
| D. | 微粒从P运动到Q机械能一定增加 |
3.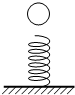 如图所示,小球从高处下落到竖直放置的轻弹簧上,在将弹簧压缩到最短的整个过程中,不计空气阻力,下列叙述中正确的是( )
如图所示,小球从高处下落到竖直放置的轻弹簧上,在将弹簧压缩到最短的整个过程中,不计空气阻力,下列叙述中正确的是( )
 如图所示,小球从高处下落到竖直放置的轻弹簧上,在将弹簧压缩到最短的整个过程中,不计空气阻力,下列叙述中正确的是( )
如图所示,小球从高处下落到竖直放置的轻弹簧上,在将弹簧压缩到最短的整个过程中,不计空气阻力,下列叙述中正确的是( )| A. | 小球的机械能守恒 | |
| B. | 重力势能和弹性势能之和先减小后增加 | |
| C. | 动能和弹性势能之和先减小后增加 | |
| D. | 重力势能与动能之和始终增大 |
10.小船在静水中行驶的速度为v0,该船船头垂直河岸行驶,下列说法中正确的是( )
| A. | 河水流速越大,小船渡河时间越长 | B. | 河水流速越大,小船渡河时间越短 | ||
| C. | 河水流速越大,小船渡河位移越大 | D. | 河水流速越大,小船渡河位移越小 |
7.已知地球同步卫星的轨道半径是地球半径的k倍,则下列说法正确的是( )
| A. | 第一宇宙速度是同步卫星运行速度的k倍 | |
| B. | 地球表面附近的重力加速度是同步卫星向心加速度的k倍 | |
| C. | 第一宇宙速度是同步卫星运行速度的$\sqrt{k}$倍 | |
| D. | 地球表面附近的重力加速度是同步卫星向心加速度的$\sqrt{k}$倍 |
4.对分子间相互作用力的理解,下面几种观点正确的是( )(填正确答案)
| A. | 0℃的冰变成0℃的水,体积要减小,表明该过程分子间的作用力为引力 | |
| B. | 0℃的冰变成0℃的水,体积虽减小,但是该过程分子间的作用力为斥力 | |
| C. | 当分子力表现为斥力时,分子势能随分子间距离的减小面增大 | |
| D. | 液体能够流动而固体不能,说明液体分子间作用力小于固体分子间作用力 | |
| E. | 固体发生形变时产生的弹力,本质上是固体大量分子间作用力的宏观表现 |
5. 哈尔滨冰雪节上有一个“高山冰车”游乐项目:冰山两侧是倾角不同的光滑冰面,游客坐在冰车上从顶端滑到水平地面,体验极速的刺激.若两名质量相同的游客同时从处于同一高度的两顶端分别沿两侧冰面由静止滑下,则( )
哈尔滨冰雪节上有一个“高山冰车”游乐项目:冰山两侧是倾角不同的光滑冰面,游客坐在冰车上从顶端滑到水平地面,体验极速的刺激.若两名质量相同的游客同时从处于同一高度的两顶端分别沿两侧冰面由静止滑下,则( )
 哈尔滨冰雪节上有一个“高山冰车”游乐项目:冰山两侧是倾角不同的光滑冰面,游客坐在冰车上从顶端滑到水平地面,体验极速的刺激.若两名质量相同的游客同时从处于同一高度的两顶端分别沿两侧冰面由静止滑下,则( )
哈尔滨冰雪节上有一个“高山冰车”游乐项目:冰山两侧是倾角不同的光滑冰面,游客坐在冰车上从顶端滑到水平地面,体验极速的刺激.若两名质量相同的游客同时从处于同一高度的两顶端分别沿两侧冰面由静止滑下,则( )| A. | 两人到达斜面底端时的速度相同 | |
| B. | 两人到达斜面底端时的动能相同 | |
| C. | 两人下滑过程中重力做功的平均功率相同 | |
| D. | 两人到达斜面底端时重力的瞬时功率相同 |
 一根长为L的均匀细杆OA可以绕水平轴O在竖直平面内转动.杆最初在水平位置,杆上距O点$\frac{\sqrt{3}}{2}$L处放一小物体m(可视为质点),杆与小物体最初处于静止状态,如图所示.若此杆突然以角速度ω绕轴O顺时针匀速转动,问ω取什么值时,杆OA与小物体可再次相碰?已知重力加速度为g.
一根长为L的均匀细杆OA可以绕水平轴O在竖直平面内转动.杆最初在水平位置,杆上距O点$\frac{\sqrt{3}}{2}$L处放一小物体m(可视为质点),杆与小物体最初处于静止状态,如图所示.若此杆突然以角速度ω绕轴O顺时针匀速转动,问ω取什么值时,杆OA与小物体可再次相碰?已知重力加速度为g.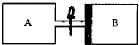 如图所示,导热材料制成的截面积相等,长度均为L=45cm的气缸A、B通过带有阀门的管道连接,初始时阀门K关闭,厚度不计的质量为m=24kg,面积S=20cm2光滑活塞C位于B内下侧,在A内充满压强PA=2×105Pa的理想气体,B内充满压强PB=1×105Pa的同种理想气体,忽略连接气缸的管道体积,室温不变,现打开阀门,求最终平衡时活塞向上移动的距离?
如图所示,导热材料制成的截面积相等,长度均为L=45cm的气缸A、B通过带有阀门的管道连接,初始时阀门K关闭,厚度不计的质量为m=24kg,面积S=20cm2光滑活塞C位于B内下侧,在A内充满压强PA=2×105Pa的理想气体,B内充满压强PB=1×105Pa的同种理想气体,忽略连接气缸的管道体积,室温不变,现打开阀门,求最终平衡时活塞向上移动的距离?