题目内容
5.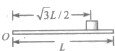 一根长为L的均匀细杆OA可以绕水平轴O在竖直平面内转动.杆最初在水平位置,杆上距O点$\frac{\sqrt{3}}{2}$L处放一小物体m(可视为质点),杆与小物体最初处于静止状态,如图所示.若此杆突然以角速度ω绕轴O顺时针匀速转动,问ω取什么值时,杆OA与小物体可再次相碰?已知重力加速度为g.
一根长为L的均匀细杆OA可以绕水平轴O在竖直平面内转动.杆最初在水平位置,杆上距O点$\frac{\sqrt{3}}{2}$L处放一小物体m(可视为质点),杆与小物体最初处于静止状态,如图所示.若此杆突然以角速度ω绕轴O顺时针匀速转动,问ω取什么值时,杆OA与小物体可再次相碰?已知重力加速度为g.
分析 当杆转动之后,小物体B将沿竖直方向自由下落.B若与杆相碰撞,一种情况是B追上杆相碰,一种情况是杆转一圈后追上B相碰,结合结合关系,抓住时间相等求出转动的角速度.
解答 解:小物体做自由落体运动,杆OA与小物体再次相遇有两种情况,
一是小物体追上杆,二是杆转动一周后追上小物体,
当两者刚好再次相碰时,对小物体有:h=$\frac{g{t}^{2}}{2}$
对细杆OA有:θ=ω1t 或θ+2π=ω2t
由几何关系知:θ=$\frac{π}{6}$,h=$\frac{L}{2}$
得ω1=$\frac{π}{6}\sqrt{\frac{g}{L}}$或ω2=$\frac{13π}{6}\sqrt{\frac{g}{L}}$
故欲使小物体和杆再次相遇必有ω≤$\frac{π}{6}\sqrt{\frac{g}{L}}$或ω≥$\frac{13π}{6}\sqrt{\frac{g}{L}}$
答:欲使小物体和杆再次相遇必有ω≤$\frac{π}{6}\sqrt{\frac{g}{L}}$或ω≥$\frac{13π}{6}\sqrt{\frac{g}{L}}$.
点评 解决本题的关键知道:
(1)杆突然转动后,小木块做自由落体运动.如果在杆转动的时间t内,杆端A恰好转到小物体的正下方使小物体与杆端相碰,即杆转过θ角的时间与小物体自由下落高度h的时间相等.
(2)求杆转动的角速度的范围.要求杆转动的角速度的临界值,就是要求两者恰好相碰时杆所转动的角速度.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
2.以下关于滑动摩擦力的说法正确的是( )
| A. | 只有运动的物体才可能受到滑动摩擦力 | |
| B. | 滑动摩擦力的方向总是与物体的运动方向相反 | |
| C. | 滑动摩擦力总是阻碍物体的运动的阻力 | |
| D. | 滑动摩擦力的方向总是与物体的相对运动方向相反 |
3.电场中有一点P,则( )
| A. | 若该处场强不为零,但该处试探电荷受电场力作用可能为零 | |
| B. | 若该处场强越大,则对于同一试探电荷在该处所受电场力越大 | |
| C. | 若该处没有试探电荷,则该处场强为零 | |
| D. | 该处的电场强度的方向就是该处试探电荷所受力的方向 |
10.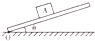 如图所示,物块A静止放在倾角为θ的长木板上,现使木板绕O点逆时针方向缓慢旋转,旋转时物块A与木板保持相对静止,则下列对于物块A的受力情况的说法中正确的是( )
如图所示,物块A静止放在倾角为θ的长木板上,现使木板绕O点逆时针方向缓慢旋转,旋转时物块A与木板保持相对静止,则下列对于物块A的受力情况的说法中正确的是( )
 如图所示,物块A静止放在倾角为θ的长木板上,现使木板绕O点逆时针方向缓慢旋转,旋转时物块A与木板保持相对静止,则下列对于物块A的受力情况的说法中正确的是( )
如图所示,物块A静止放在倾角为θ的长木板上,现使木板绕O点逆时针方向缓慢旋转,旋转时物块A与木板保持相对静止,则下列对于物块A的受力情况的说法中正确的是( )| A. | 木板对物块A的作用力不变 | B. | 木板对物块A的作用力变小 | ||
| C. | 木板对物块A的支持力变大 | D. | 木板对物块A的摩擦力变小 |
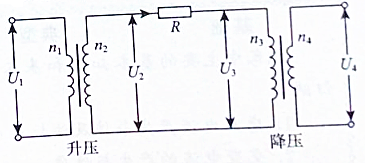
17.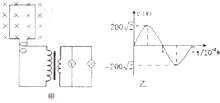 如图甲所示,电阻不计的矩形线框绕垂直于匀强磁场的轴以角速度ω匀速转动,产生了如图乙所示的正弦交变电流.理想变压器的原副线圈匝数之比为10:1,
如图甲所示,电阻不计的矩形线框绕垂直于匀强磁场的轴以角速度ω匀速转动,产生了如图乙所示的正弦交变电流.理想变压器的原副线圈匝数之比为10:1, 为交流电压表,灯泡的电阻RL=10Ω,以下说法正确的是( )
为交流电压表,灯泡的电阻RL=10Ω,以下说法正确的是( )
 如图甲所示,电阻不计的矩形线框绕垂直于匀强磁场的轴以角速度ω匀速转动,产生了如图乙所示的正弦交变电流.理想变压器的原副线圈匝数之比为10:1,
如图甲所示,电阻不计的矩形线框绕垂直于匀强磁场的轴以角速度ω匀速转动,产生了如图乙所示的正弦交变电流.理想变压器的原副线圈匝数之比为10:1, 为交流电压表,灯泡的电阻RL=10Ω,以下说法正确的是( )
为交流电压表,灯泡的电阻RL=10Ω,以下说法正确的是( )| A. | 通过小灯泡的电流的频率为5Hz | |
| B. | t=0.Ols时刻,电压表的示数为0 | |
| C. | t=0.O1s时刻,穿过矩形线框的磁通量最大 | |
| D. | 灯泡在1分钟内发热2400J |
14. 如图所示,在绝缘粗糙水平面上固定两个等量同种电荷P、Q,在PQ连线上更靠近P的M点由静止释放一带电滑块,则滑块会由静止开始一直向右运动到PQ连线上的另一点N而停下.下述正确的是( )
如图所示,在绝缘粗糙水平面上固定两个等量同种电荷P、Q,在PQ连线上更靠近P的M点由静止释放一带电滑块,则滑块会由静止开始一直向右运动到PQ连线上的另一点N而停下.下述正确的是( )
 如图所示,在绝缘粗糙水平面上固定两个等量同种电荷P、Q,在PQ连线上更靠近P的M点由静止释放一带电滑块,则滑块会由静止开始一直向右运动到PQ连线上的另一点N而停下.下述正确的是( )
如图所示,在绝缘粗糙水平面上固定两个等量同种电荷P、Q,在PQ连线上更靠近P的M点由静止释放一带电滑块,则滑块会由静止开始一直向右运动到PQ连线上的另一点N而停下.下述正确的是( )| A. | 滑块受到的电场力一定是先减小后增大 | |
| B. | 停下前滑块的加速度一定是先减小后增大 | |
| C. | 滑块的动能与电势能之和保持不变 | |
| D. | PM间距一定小于QN间距 |




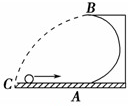 如图所示,一光滑的半径为R的半圆形竖直轨道AB固定在水平面上.一个质量为m的小球以某一速度冲上轨道,然后小球从轨道口B处水平飞出,最后落在水平面上,已知小球落地点C距B处的水平距离为3R.求:
如图所示,一光滑的半径为R的半圆形竖直轨道AB固定在水平面上.一个质量为m的小球以某一速度冲上轨道,然后小球从轨道口B处水平飞出,最后落在水平面上,已知小球落地点C距B处的水平距离为3R.求: