题目内容
5.一颗小行星的半径为128Km,它的密度与地球的密度相同,已知地球半径为6400km,地球的第一宇宙速度为8km/s,则该小行星的第一宇宙速度为160m/s.分析 第一宇宙速度又称为环绕速度,是指在地球上发射的物体绕地球飞行作圆周运动所需的最小初始速度,是人造地球卫星在圆轨道上运行的最大速度;根据万有引力提供向心力列式求解.
解答 解:已知地球半径为R=6400km,地球上第一宇宙速度为V=8km/s,密度为ρ,小行星的半径为128km,
根据万有引力提供向心力得:则有G$\frac{mM}{{R}^{2}}$=m$\frac{{V}^{2}}{R}$,
M=ρ$\frac{4}{3}$πR3,
解得:V=$\sqrt{\frac{GM}{R}}$=2R$\sqrt{\frac{Gπρ}{3}}$ ①
小行星的第一宇宙速度表达式为:v1=2r$\sqrt{\frac{Gπρ}{3}}$ ②
把①②两式取比值得:v1=$\frac{rV}{R}$=160m/s,
故答案为:160.
点评 本题要掌握第一宇宙速度的定义,正确利用万有引力公式列出第一宇宙速度的表达式;然后代入不同的物理量.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
13.在地面附近某一高处水平抛出一物体,若不计空气阻力,则物体在空中的运动是( )
| A. | 匀变速运动 | B. | 变加速运动 | C. | 匀速率运动 | D. | 一段圆周运动 |
20.置于水平面上的质量为m的物体,在一水平恒力F的作用下,由静止开始做匀加速直线运动,在物体滑行一段距离S后,撤去F,物体再滑行3S的距离而停下来.物体受到的阻力的大小为F的( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
17.质量为m的滑块,从倾角为θ固定斜面顶端静止滑下,经时间t到达底端,该过程滑块重力的冲量为( )
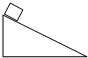

| A. | mgt 竖直向下 | B. | mgt 沿斜面向下 | ||
| C. | mgtsinθ 竖直向下 | D. | mgtsinθ 沿斜面向下 |
14.两行星运行轨迹的半长轴之比为4:9,其运行周期之比为( )
| A. | 4:9 | B. | 2:3 | C. | 8:27 | D. | 5:3 |
 一组太空人乘太空穿梭机去修理位于离地球表面6.0×105m的圆形轨道上的哈勃太空望远镜H.机组人员驾驶穿梭机S进入与H相同的轨道并关闭推动火箭,而望远镜在穿梭机前方数千米处,如图所示.引力常量为G,地球质量为ME(已知地球半径为R=6.4×106m,地球表面的重力加速度g=9.8m/s2)
一组太空人乘太空穿梭机去修理位于离地球表面6.0×105m的圆形轨道上的哈勃太空望远镜H.机组人员驾驶穿梭机S进入与H相同的轨道并关闭推动火箭,而望远镜在穿梭机前方数千米处,如图所示.引力常量为G,地球质量为ME(已知地球半径为R=6.4×106m,地球表面的重力加速度g=9.8m/s2) 如图,放在水平地面上的瓶子质量为M,瓶中压缩气体密度为ρ,瓶口横截面积为S,地面与瓶间摩擦系数为μ,当打开瓶塞气体以速度v喷出时瓶子的加速度大小为多少?
如图,放在水平地面上的瓶子质量为M,瓶中压缩气体密度为ρ,瓶口横截面积为S,地面与瓶间摩擦系数为μ,当打开瓶塞气体以速度v喷出时瓶子的加速度大小为多少?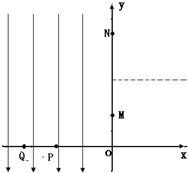 如图所示,xOy平面内,y轴左侧存在着沿y轴负方向的匀强电场,y轴右侧直线y=2a(图中虚线)上方存在着一个匀强磁场区域,磁场方向垂直xOy平面(图中未画出).一个质量为m、带电荷量为+q的粒子从坐标P(-2a,0)以速度v0沿x轴正方向开始运动.经过M(0,a)点进入y轴右侧,通过磁场区域后,从N点垂直经过y轴第二次进入电场时,电场反向场,强大小不变.不计粒子的重力,试求:
如图所示,xOy平面内,y轴左侧存在着沿y轴负方向的匀强电场,y轴右侧直线y=2a(图中虚线)上方存在着一个匀强磁场区域,磁场方向垂直xOy平面(图中未画出).一个质量为m、带电荷量为+q的粒子从坐标P(-2a,0)以速度v0沿x轴正方向开始运动.经过M(0,a)点进入y轴右侧,通过磁场区域后,从N点垂直经过y轴第二次进入电场时,电场反向场,强大小不变.不计粒子的重力,试求: