题目内容
 如图所示,AB是倾角为θ的粗糙直轨道,BECD是圆心为O的光滑圆轨道,半径为R,与AB在B点相切.一质量为m质点,从直轨道上P点由静止释放,P、O、C三点在同一水平直线上,E为最低点,质点与AB直轨道动摩擦因数为μ,重力加速度为g,求:
如图所示,AB是倾角为θ的粗糙直轨道,BECD是圆心为O的光滑圆轨道,半径为R,与AB在B点相切.一质量为m质点,从直轨道上P点由静止释放,P、O、C三点在同一水平直线上,E为最低点,质点与AB直轨道动摩擦因数为μ,重力加速度为g,求:(1)质点第一次通过E点向左运动时轨道对其支持力大小;
(2)质点在AB直轨道上运动的最大路程(质点没有脱离原轨道);
(3)为了不脱离轨道在轨道上往复运动,则释放点改为P'点,则P'点离B的点距离最大不超过多少?
分析:(1)质点从P运动到E过程,根据动能定理求出质点通过E点时的速度大小.质点经过E点时,由重力和轨道的支持力的合力提供向心力,根据牛顿第二定律求解轨道的支持力大小;
(2)由于质点在粗糙斜面滑动时机械能不断减少,最终质点在以B点为最高点的圆弧上往复运动,通过B点的速度为零,对全过程,根据动能定理求出质点在AB直轨道上运动的最大路程;
(3)为了不脱离轨道在轨道上往复运动,质点运动的最高点为C点且速度vC=0,根据动能定理求解P'点离B的点的距离.
(2)由于质点在粗糙斜面滑动时机械能不断减少,最终质点在以B点为最高点的圆弧上往复运动,通过B点的速度为零,对全过程,根据动能定理求出质点在AB直轨道上运动的最大路程;
(3)为了不脱离轨道在轨道上往复运动,质点运动的最高点为C点且速度vC=0,根据动能定理求解P'点离B的点的距离.
解答:解:(1)根据动能定理得:
从P→E:mgR-μmgcosθ?Rcotθ=
m
在E点:FN-mg=m
联立解得,FN=mg(3-2μcosθcotθ)
(2)最终通过B点时速度为O,对整个过程,运用动能定理得
mgRcosθ-μmgcosθ?S总=0
解得,S总=
(3)为了不脱离轨道在轨道上往复运动,质点运动的最高点为C点且速度vC=0,
则 mg(Lsinθ-Rcosθ)-μmgcosθ?L=0
有:L=
=
答:(1)质点第一次通过E点向左运动时轨道对其支持力大小是mg(3-2μcosθcotθ);
(2)质点在AB直轨道上运动的最大路程是
;
(3)为了不脱离轨道在轨道上往复运动,释放点改为P'点,则P'点离B的点距离最大不超过
.
从P→E:mgR-μmgcosθ?Rcotθ=
| 1 |
| 2 |
| v | 2 E |
在E点:FN-mg=m
| ||
| R |
联立解得,FN=mg(3-2μcosθcotθ)
(2)最终通过B点时速度为O,对整个过程,运用动能定理得
mgRcosθ-μmgcosθ?S总=0
解得,S总=
| R |
| μ |
(3)为了不脱离轨道在轨道上往复运动,质点运动的最高点为C点且速度vC=0,
则 mg(Lsinθ-Rcosθ)-μmgcosθ?L=0
有:L=
| Rcosθ |
| sinθ-μcosθ |
| R |
| tanθ-μ |
答:(1)质点第一次通过E点向左运动时轨道对其支持力大小是mg(3-2μcosθcotθ);
(2)质点在AB直轨道上运动的最大路程是
| R |
| μ |
(3)为了不脱离轨道在轨道上往复运动,释放点改为P'点,则P'点离B的点距离最大不超过
| R |
| tanθ-μ |
点评:本题综合应用了动能定理、圆周运动及圆周运动中能过最高点的条件,关键要抓住滑动摩擦力做功与总路程有关.

练习册系列答案
相关题目
 如图所示,AB是倾角为θ的粗糙直轨道,BCD是光滑的圆弧轨道,AB恰好在B点与圆弧相切,圆弧的半径为R.一个质量为m的物体(可视为质点)从直轨道的P点由静止释放,结果它在两轨道之间做往复运动.已知P点与圆弧的圆心O等高,物体与轨道AB间的动摩擦因素为μ,求:
如图所示,AB是倾角为θ的粗糙直轨道,BCD是光滑的圆弧轨道,AB恰好在B点与圆弧相切,圆弧的半径为R.一个质量为m的物体(可视为质点)从直轨道的P点由静止释放,结果它在两轨道之间做往复运动.已知P点与圆弧的圆心O等高,物体与轨道AB间的动摩擦因素为μ,求: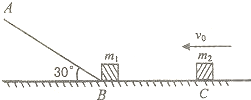 如图所示,AB是倾角为30°足够长的光滑斜面,BC是足够长的光滑水平面,且在B点与斜面平滑连接,质量m1=0.2kg的滑块嚣于B点,质量m2=0.1kg的滑块以v0=9m/s速度向左运动并与m1发生撞碰,碰撞过程中没有机械能损失,且ml通过B点前后速率不变,将滑块视为质点,以下判断正确的是(g=10m/s2)( )
如图所示,AB是倾角为30°足够长的光滑斜面,BC是足够长的光滑水平面,且在B点与斜面平滑连接,质量m1=0.2kg的滑块嚣于B点,质量m2=0.1kg的滑块以v0=9m/s速度向左运动并与m1发生撞碰,碰撞过程中没有机械能损失,且ml通过B点前后速率不变,将滑块视为质点,以下判断正确的是(g=10m/s2)( ) 如图所示,AB是倾角θ为45°的直轨道,CD是半径R=0.4m圆弧轨道,它们通过一段曲面BC平滑相接,整个轨道处于竖直平面内且处处光滑.一个质量m=1kg的物体(可以看作质点)从高H的地方由静止释放,结果它从圆弧最高点D点飞出,垂直斜面击中P点.已知P点与圆弧的圆心O等高.求:(取g=10m/s2)
如图所示,AB是倾角θ为45°的直轨道,CD是半径R=0.4m圆弧轨道,它们通过一段曲面BC平滑相接,整个轨道处于竖直平面内且处处光滑.一个质量m=1kg的物体(可以看作质点)从高H的地方由静止释放,结果它从圆弧最高点D点飞出,垂直斜面击中P点.已知P点与圆弧的圆心O等高.求:(取g=10m/s2)