��Ŀ����
����Ŀ����ͼ,�⻬�ĵ�������һ����Ϊm����ֱƽ���ڵĹ��ABC�������ķ�֮һԲ������Բ���¶����е�ˮƽ���ֹ��ɡ�A��B����Բ���������ߵ����͵㡣��֪�����Բ�����ֹ⻬,�뾶ΪR����ˮƽ���ֲִڣ��뻬�鶯Ħ������Ϊ�����ֽ�һ����ҲΪm�����A�㾲ֹ�ͷš�ȡ�������ٶ�g=10m/s2����:
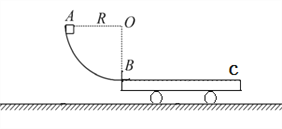
(1)���龲ֹ�ͷź��˶���B����ٶȡ�
(2)Ϊ��ʹ���鲻�ӹ���ϵ���ȥ�������ˮƽ���ֳ���L�����Ƕ��١�
���𰸡���1��![]() ��2��
��2��![]()
����������1�������Բ������»��Ĺ����У������С��ϵͳ��ˮƽ�������غ㣬������B��ʱ���ɶ����غ㶨�ɣ�0=mv1+mv2����v1=v2.��A��B��ϵͳ�ɻ�е���غ㶨�ɿ�֪��![]() ��ã�
��ã�![]()
��2����黬��С�������ﵽ��ͬ�ٶ�ʱ������Ծ�ֹ�����ʱ�Ĺ�ͬ�ٶ�Ϊv�����������ߵ㻬�µ����С����ֹ�����������У��ɶ����غ㶨�ɣ�0=2mv, ��֪���������ٶȾ�Ϊ�㣬����������ϵ��֪��mgR=mgL��
���![]()

��ϰ��ϵ�д�
 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д� ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д� �㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�����Ŀ