Question

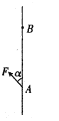
【题目】如图，用0.4m长的轻杆拴住一质量为1kg的小球在竖直面内绕O点做圆周运动，小球通过最低点A时的速度大小为m/s，小球通过最高点B时杆中的弹力为零（g = 10m/s2）。求：

⑴小球通过A点时轻杆对小球的弹力；

⑵小球通过B点时的速度大小；

⑶若小球通过B点时速度大小为1m/s，轻杆对小球的弹力。

Answer 1

【答案】⑴60N，方向竖直向上　⑵2m/s　⑶7.5N

【解析】

抓住小球恰好通过最高点，绳子拉力为零，结合牛顿第二定律求出A点的速度，在最低点，根据拉力和重力的合力提供向心力求出拉力的大小，根据高度求出平抛运动的时间，结合初速度和时间求出水平位移。

(1) 小球通过最低点A时，由重力和轻杆拉力的合力提供小球做圆周运动的向心力，由牛顿第二定律：

得：

代入可得：T1=60N，方向竖直向上；

(2) 小球通过最高点B时，小球重力提供向心力，根据牛顿第二定律得：

代入得：v２= 2m/s；

(3) 小球通过最高点B时，v3= 1m/s＜2m/s，轻杆对小球的弹力方向竖直向上

得：

代入可得：T2=7.5N。