题目内容
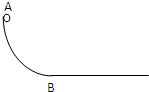如图中圆弧轨道AB是在竖直平面内的以R为半径的| 1 | 4 |
2g
2g
，刚滑过B点时的加速度大小为0
0
．分析：质点刚要到达B点时，受重力和支持力，两个力的合力提供向心力，根据牛顿第二定律求出加速度大小．滑过B点时所受的合力为零，根据牛顿第二定律可知加速度为零．
解答：解：质点刚要到达B点时，有F合=m
=ma1
根据动能定理得：mgR=
mv2
解得：a1=2g
滑过B点时受重力和支持力，所受的合力为零，根据牛顿第二定律可知加速度为零，即a2=0．
故答案为：2g；0．
| v2 |
| R |
根据动能定理得：mgR=
| 1 |
| 2 |
解得：a1=2g
滑过B点时受重力和支持力，所受的合力为零，根据牛顿第二定律可知加速度为零，即a2=0．
故答案为：2g；0．
点评：解决本题的关键知道质点刚要到达B点时，受重力和支持力，两个力的合力提供向心力．滑过B点时所受的合力为0．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，AB是倾角为θ的粗糙直轨道，BCD是光滑的圆弧轨道，AB恰好在B点与圆弧相切，圆弧的半径为R．一个质量为m的物体（可以看作质点）从直轨道上的P点由静止释放，结果它能在两轨道间做往返运动．已知P点与圆弧的圆心O等高，物体与轨道AB间的动摩擦因数为μ．求：
如图所示，水平光滑地面上停放着一辆质量为M的小车，小车左端靠在竖直墙壁上，其左侧半径为R的四分之一圆弧轨道AB是光滑的，轨道最低点B与水平轨道BC相切，整个轨道处于同一竖直平面内．将质量为m的物块（可视为质点）从A点无初速度释放，物块沿轨道滑行至轨道末端C处恰好没有滑出．重力加速度为g，空气阻力可忽略不计．关于物块从A位置运动至C位置的过程，下列说法中正确的是（ ）
（2005?盐城模拟）如图所示，AB是一倾角为θ=37°的光滑直轨道，BCD是半径为R=0.5m的光滑圆弧轨道，它们相切于B点，C为圆弧轨道的最低点，D为其最高点，A、C两点间的高度差为h=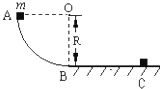
如图所示，AB是竖直面内的四分之一圆弧形光滑轨道，下端B与水平直轨道相切．一个小物块自A点由静止开始沿轨道下滑，已知轨道半径为R=0.2m，小物块的质量为m=0.1kg，小物块与水平面间的动摩擦因数?=0.5，取g=10m/s2．求：