题目内容
【题目】如图所示,等腰直角三角形ABC为某透明介质的横截面。O为BC边的中点,位于O点处的点光源在透明介质内向各个方向发射光线,其中OD光线与OC夹角15°,从AC边上的D点射出的光线平行于BC,从E点射出的光线垂直BC向上。已知BC边长2L.求:
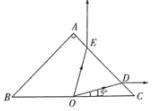
①该介质的折射率;
②光从O点传到E点的时间。
【答案】![]()
【解析】
光路图如图所示:
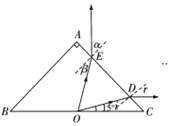
①做出法线,由几何关系知从D射出的光线的折射角r=45°
入射角i=30°,根据折射定律得:![]()
②过E点做法线,由几何关系得:α=r=45°
由折射定律![]() 得:β=i=30°
得:β=i=30°
由几何关系得:∠OED=60°,∠EDO=60°,△ODE为等边三角形,即OE=OD,
在△ODC中由正弦定理得![]() 解得:
解得:![]()
光在介质中的传播速度![]() 光在介质中的传播时间
光在介质中的传播时间![]() 联立解得:
联立解得:![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目