��Ŀ����
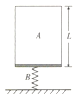
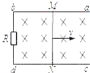
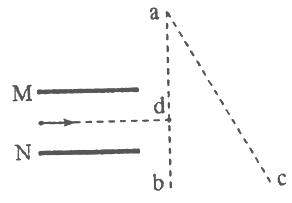
����Ŀ����ͼ��ʾ��M��NΪˮƽ���õ�����ƽ�н����壬����ΪL�������������ֱ����ǿ�糡����ǿ�ų������Ʋ�Ϊ![]() ���Ÿ�Ӧǿ�ȴ�СΪ
���Ÿ�Ӧǿ�ȴ�СΪ![]() .һ������������Ӵ������е㴹ֱ�������ĵ硢�ų�ˮƽ���룬��ֱ��ͨ�������壬������ab��ֱ�ķ�����d�������ͼ��ʾ�������Ե�ų��ı�ԵЧӦ����ֱ�߽߱�ab��ac��ͬһ��ֱƽ���ڣ�����ab��ac���������㹻��������������
.һ������������Ӵ������е㴹ֱ�������ĵ硢�ų�ˮƽ���룬��ֱ��ͨ�������壬������ab��ֱ�ķ�����d�������ͼ��ʾ�������Ե�ų��ı�ԵЧӦ����ֱ�߽߱�ab��ac��ͬһ��ֱƽ���ڣ�����ab��ac���������㹻��������������![]() ����
����
(1)���������������ٶȴ�С��
(2)��bac��������ڴ�ֱֽ�����ڵ���ǿ�ų���Ҫʹ���Ӳ���ac�߽����������С�Ÿ�Ӧǿ��ΪB 1����bac�����ڽ�����ƽ��ֽ����ƽ��ab�������µ���ǿ�糡��Ҫʹ���Ӳ���ac�����������С�糡ǿ��ΪE1.��B1��E1�ı�ֵΪ����?
���𰸡���1��v=![]() ��2��
��2��![]()
��������
(1)��������ӵ����Ϊq������Ϊm������������ٶ�Ϊv��������ֱ���˶�ʱ�糡������������ƽ�⣬����ƽ�������У�qvB0= qE0 ��
E0 =![]() ��
��
���:v=![]() ��
��
(2)��������ǿ�ų�ʱ�����������Ӹպò���ac�����������켣Բ��ac�����У���
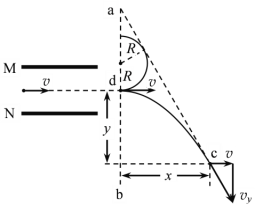
![]() ��
��
qvB1 =![]() ��
��
��:B1=![]() ��
��
��������ǿ�糡ʱ�������Ӳ���ac������������ӵ���߽���ac��ĩ�ٶ�Ҳ����ac�����У����� x=vt ��
y=![]() at2 ��
at2 ��
qE1=ma ��
tan30=![]() ��
��
![]() ��
��
tan30 =![]() ��
��
��:E1=![]() ��
��
����:![]() ��
��