题目内容
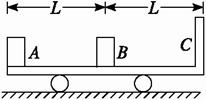
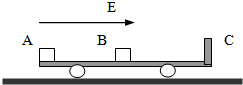 长为2L的板面光滑且不导电的平板车C放在光滑水平地面上,车的右端有一块挡板,车的质量为mC=4m,绝缘物体B的质量为mB=2m,B位于车板面的中间,带电的金属块A的质量mA=1m,所带电荷量为+q,A、B开始处于图示位置而静止,今在整个空间加一水平向右的匀强电场,金属块A由静止开始向右运动,与B发生碰撞时的速度为v0,碰后A以v0/4的速度反弹回来,B向右运动(设A、B均可看作质点,且碰撞中无电荷量的转移,若B与C相碰,则碰后C的速度等于碰前B的速度的一半).
长为2L的板面光滑且不导电的平板车C放在光滑水平地面上,车的右端有一块挡板,车的质量为mC=4m,绝缘物体B的质量为mB=2m,B位于车板面的中间,带电的金属块A的质量mA=1m,所带电荷量为+q,A、B开始处于图示位置而静止,今在整个空间加一水平向右的匀强电场,金属块A由静止开始向右运动,与B发生碰撞时的速度为v0,碰后A以v0/4的速度反弹回来,B向右运动(设A、B均可看作质点,且碰撞中无电荷量的转移,若B与C相碰,则碰后C的速度等于碰前B的速度的一半).(1)求匀强电场场强的大小;
(2)若A第二次与B相碰,试通过计算判断是在B与C相碰之前还是相碰之后;
(3)A从第一次与B相碰到第二次与B相碰的过程中,电场力对A做了多少功?
分析:1)物体A与B碰撞前受重力、电场力和支持力,根据动能定理列式可以求出电场强度的大小和方向;
(2)对于物体A、B的第一次碰撞过程,动量守恒,求出碰撞后各自的速度,此后B做匀速运动,A做先减速向左后向右加速运动,根据运动学公式列式判断即可;
(3)先根据运动学公式求解出物体A运动的总位移,然后根据功的定义列式求解.
(2)对于物体A、B的第一次碰撞过程,动量守恒,求出碰撞后各自的速度,此后B做匀速运动,A做先减速向左后向右加速运动,根据运动学公式列式判断即可;
(3)先根据运动学公式求解出物体A运动的总位移,然后根据功的定义列式求解.
解答:解:(1)A在电场力作用下向右运动,A所受电场力向右,
A与B碰撞前对A,由动能定理得,qEl=
mv02,
代入数据解得:E=
(1)A、B相碰,mv0=-m
+2mvB,
vB=
v0
B以
向右匀速运动,而A以初速度
、加速度a=
向右加速运动,设再次相遇有
v0t=-
t+
t2,则t=
,
在这段时间内B的位移sB=
v0×
=
L>L.
所以A与B第二次相碰应发生在B与C碰后.
(3)B匀速运动L与C相碰时间,t1=
=
,
碰中:2mvB=2m
+4m?
v0,vB′=0.
碰后B静止不动,而A在电场力作用下加速,直至与B相碰,不难看出,在这段时间内A的位移为L,电场力做功W=qEL=
mv02.
答:(1)匀强电场场强的大小E=
;
(2)通过计算得出:A与B第二次相碰应发生在B与C碰后;
(3)电场力对A做功为
m
.
A与B碰撞前对A,由动能定理得,qEl=
| 1 |
| 2 |
代入数据解得:E=
| mv02 |
| 2qL |
(1)A、B相碰,mv0=-m
| v0 |
| 4 |
vB=
| 5 |
| 8 |
B以
| 5v0 |
| 8 |
| -v0 |
| 4 |
| qE |
| m |
向右加速运动,设再次相遇有
| 5 |
| 8 |
| v0 |
| 4 |
| 1 |
| 2 |
| qE |
| m |
| 28L |
| 8v0 |
在这段时间内B的位移sB=
| 5 |
| 8 |
| 28L |
| 8v0 |
| 35 |
| 16 |
所以A与B第二次相碰应发生在B与C碰后.
(3)B匀速运动L与C相碰时间,t1=
| L | ||
|
| 8L |
| 5v0 |
碰中:2mvB=2m
| v | ′ B |
| 5 |
| 16 |
碰后B静止不动,而A在电场力作用下加速,直至与B相碰,不难看出,在这段时间内A的位移为L,电场力做功W=qEL=
| 1 |
| 2 |
答:(1)匀强电场场强的大小E=
| mv02 |
| 2qL |
(2)通过计算得出:A与B第二次相碰应发生在B与C碰后;
(3)电场力对A做功为
| 1 |
| 2 |
| v | 2 0 |
点评:本题关键是分析清楚各个物体的运动情况,然后动量守恒定律、动能定理和运动学公式多次列式分析求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
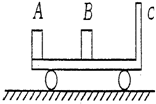 如图所示,长为2L的板面光滑且不导电的平板小车C放在光滑水平面上,车的右端有档板,车的质量mC=4m.今在静止的平板车的左端放一个带电量为+q.质量为m的物块A,在中间位置放一个绝缘物体B,质量为mB=2m.在整个空间加上一个水平方向的匀强电场时,金属块A由静止开始向右运动,并以速度v0与B发生碰撞,碰后A以
如图所示,长为2L的板面光滑且不导电的平板小车C放在光滑水平面上,车的右端有档板,车的质量mC=4m.今在静止的平板车的左端放一个带电量为+q.质量为m的物块A,在中间位置放一个绝缘物体B,质量为mB=2m.在整个空间加上一个水平方向的匀强电场时,金属块A由静止开始向右运动,并以速度v0与B发生碰撞,碰后A以 (2005?深圳一模)如图所示,长为2L的板面光滑且不导电的平板小车C放在光滑水平面上,车的右端有挡板,车的质量mC=4m.今在静止的平板车的左端放一个带电荷量为+q、质量为mA=m的金属块A,另将一绝缘小物块B放在平板车的中央,物块B的质量mB=2m.在整个空间加上一个水平方向的匀强电场时,金属块A由静止开始向右运动,A以速度v0与B发生碰撞,碰后A以v0/4的速度反弹回来,B以一定速度沿平板向右运动与C车的挡板相碰.碰后小车的速度等于碰前物块B速度的一半.物块A、B均视为质点,A、B相碰时的相互作用力远大于电场力.求:
(2005?深圳一模)如图所示,长为2L的板面光滑且不导电的平板小车C放在光滑水平面上,车的右端有挡板,车的质量mC=4m.今在静止的平板车的左端放一个带电荷量为+q、质量为mA=m的金属块A,另将一绝缘小物块B放在平板车的中央,物块B的质量mB=2m.在整个空间加上一个水平方向的匀强电场时,金属块A由静止开始向右运动,A以速度v0与B发生碰撞,碰后A以v0/4的速度反弹回来,B以一定速度沿平板向右运动与C车的挡板相碰.碰后小车的速度等于碰前物块B速度的一半.物块A、B均视为质点,A、B相碰时的相互作用力远大于电场力.求: