��Ŀ����
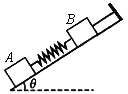
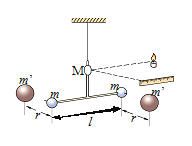
����Ŀ����ͼ��ʾ,�̶��⻬����������ΪL,������費��,�϶�a��b�������ֵΪR�ĵ���,����ƽ����ˮƽ��ļн�Ϊ��,�Ҵ��ڴŸ�Ӧǿ�ȴ�СΪB. ����ֱ�ڵ���ƽ�����ϵ���ǿ�ų��С�����Ϊm������Ϊr�ĵ������̶�������������ڵ����ϡ���ʼʱ��,����ǡ������Ȼ����,����������ع�����ϵij��ٶ�v0.�����˶������е����ʼ���뵼�촹ֱ���������ýӴ�����֪���ɵľ���ϵ��Ϊk�����ɵ����������뵼��ƽ�С�

(1)���ʼʱ��ͨ������R�ĵ���I�Ĵ�С�ͷ���
(2)���������һ�λص���ʼλ��ʱ���ٶȱ�Ϊv�����ʱ������ļ��ٶȴ�Сa.
���𰸡���1��![]() ��������Ϊb��a ��2��gsin��
��������Ϊb��a ��2��gsin��![]()
������������������������˶��и�Ÿ��ߣ���E=BLv���Ӧ�綯�ƣ���ŷķ�������Ӧ�������������ֶ����жϸ�Ӧ�����ķ��������������һ�λص���ʼλ��ʱ���ٶȱ�Ϊv���������ĸ�Ӧ�綯��ΪE=BLv������ŷķ������ø�Ӧ��������F=BIL�����ʱ�����ܵİ�����������ţ�ٵڶ����ɾͿ���������ٶ���
(1)�������ĸ�Ӧ�綯��Ϊ��E1=BLv0
����ŷķ���ɵ�ͨ��R�ĵ�����СΪ�� ![]()
�������ֶ����жϵ�֪����������Ϊb��a
(2)�������ĸ�Ӧ�綯��Ϊ��E2=BLv
����ŷķ���ɵø�Ӧ����Ϊ�� ![]()
���ܵ��İ�������СΪ�� ![]() ��������б�����ϣ�������ͼ��ʾ��
��������б�����ϣ�������ͼ��ʾ��

����ţ�ٵڶ������У� ![]()
��ã� 

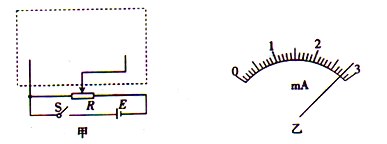
����Ŀ�����������������Dz���С����U��I��ϵ��ʵ�����ݣ�
U��V�� | 0.0 | 0.2 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
I��A�� | 0.000 | 0.050 | 0.100 | 0.150 | 0.180 | 0.195 | 0.205 | 0.215 |

��1����������ʵ�����ݿ�֪��Ӧѡ�õ�ʵ���·ͼ��ͼ�е�_____��ѡ��������������������
��2������ͼ����ʾ�ķ���ֽ�ڻ���С���ݵ�U��I����_________���������߿�֪С���ݵĵ�����I����_____��ѡ���������������С���������䣩��