题目内容
(2006?淮安二模)将一测力传感器连接到计算机上就可以测量快速变化的力.图甲表示小滑块(可视为质点)沿固定的光滑半球形容器内壁在竖直平面的AA′之间来回滑动,AA′点与O 点连线与竖直方向之间的夹角相等且都为θ,均小于10°,图乙表示滑块对器壁的压力F随时间t变化的曲线,且图中t=0为滑块从A点开始运动的时刻.试根据力学规律和题中(包括图中)所给出的信息,求小滑块的质量、容器的半径及滑块运动过程中的守恒量.(g=10m/s2)


分析:(1)θ很小,小滑块在AA′之间做简谐运动(单摆运动),根据图乙得出单摆的周期,再根据T=2π
得容器的半径;
(2)滑块在最高点,对器壁的压力最小,为Fmin=mgcosθ,在最低点速度最大,沿半径方向上的合力提供向心力,此时压力最大,则Fmax-mg=m
,最高点到最低点,机械能守恒,有
mv02=mgR(1-cosθ).联立三个式子求出滑块的质量.
(3)滑块运动过程中机械能守恒,守恒量为机械能,规定B点为0势能点,机械能等于A点的重力势能.
|
(2)滑块在最高点,对器壁的压力最小,为Fmin=mgcosθ,在最低点速度最大,沿半径方向上的合力提供向心力,此时压力最大,则Fmax-mg=m
| v02 |
| R |
| 1 |
| 2 |
(3)滑块运动过程中机械能守恒,守恒量为机械能,规定B点为0势能点,机械能等于A点的重力势能.
解答:解:(1)滑块在AA′之间做简谐运动,周期T=
s
由T=2π
得容器的半径:R=
=0.1m
(2)由牛顿第二定律,在平衡位置:Fmax-mg=m
…①
在A点时有:Fmin=mgcosθ…②
滑块由A到B过程机械能守恒得:
mv02=mgR(1-cosθ)③
其中,Fmax=0.510N;Fmin=0.495N
由①②③式解得小滑块的质量:m=0.05㎏,cosθ=0.99
(3)滑块机械能守恒,守恒量机械能E=mgR(1-cosθ)=5×10-4J
答:小滑块的质量为0.05㎏,容器的半径为0.1m,滑块运动过程中的守恒量为机械能.
| π |
| 5 |
由T=2π
|
| T2g |
| 4π2 |
(2)由牛顿第二定律,在平衡位置:Fmax-mg=m
| v02 |
| R |
在A点时有:Fmin=mgcosθ…②
滑块由A到B过程机械能守恒得:
| 1 |
| 2 |
其中,Fmax=0.510N;Fmin=0.495N
由①②③式解得小滑块的质量:m=0.05㎏,cosθ=0.99
(3)滑块机械能守恒,守恒量机械能E=mgR(1-cosθ)=5×10-4J
答:小滑块的质量为0.05㎏,容器的半径为0.1m,滑块运动过程中的守恒量为机械能.
点评:解决本题的关键知道滑块所做的运动是单摆运动,知道单摆运动的周期公式,以及知道在什么位置压力最大,什么位置压力最小,运用机械能守恒进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
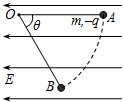 (2006?淮安二模)如图所示,在场强大小为E的匀强电场中,一根不可伸长的绝缘细线一端拴一个质量为m电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零.以下说法正确的是( )
(2006?淮安二模)如图所示,在场强大小为E的匀强电场中,一根不可伸长的绝缘细线一端拴一个质量为m电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零.以下说法正确的是( ) (2006?淮安二模)如图所示,一根不可伸长的轻绳一端拴着一个小球,另一端固定在竖直杆上,当竖直杆以角速度ω转动时,小球跟着杆一起做匀速圆周运动,此时绳与竖直方向的夹角为θ,下列关于ω与θ关系的图象正确的是( )
(2006?淮安二模)如图所示,一根不可伸长的轻绳一端拴着一个小球,另一端固定在竖直杆上,当竖直杆以角速度ω转动时,小球跟着杆一起做匀速圆周运动,此时绳与竖直方向的夹角为θ,下列关于ω与θ关系的图象正确的是( )