题目内容
（2006?淮安二模）一个用于加速质子的回旋加速器，其D形盒半径为R，垂直D形盒底面的匀强磁场的磁感应强度为B，接在D形盒上的高频电源频率为f．下列说法正确的是（ ）
分析：粒子在磁场中运动时，洛伦兹力提供向心力，满足qvB=m
，运动周期T=
=
（电场中加速时间忽略不计）．对公式进行简单推导后，便可解此题．
| v2 |
| r |
| 2πr |
| v |
| 2πm |
| Bq |
解答：解：A、根据v=
=2πRf，可知：最大半径为R，且电场变化的频率即为粒子在磁场中运动周期，所以最大速度不可能超过2πfR．故A正确，
B、根据qvB=m
得，粒子的最大速度v=
，则最大动能EKm=
mv2=
．知增大动能，需增大D形盒的半径，或增大磁感应强度，故B正确；
C、若R足够大，质子的速度不可以被加速到任意值，因当达到一定速度后，质子的质量发生变化，导致周期变化，故C错误；
D、若是α粒子，则粒子的比荷发生变化，所以周期也变化，因此不能用这个装置，故D错误，
故选AB．
| 2πR |
| T |
B、根据qvB=m
| v2 |
| R |
| qBR |
| m |
| 1 |
| 2 |
| q2B2R2 |
| 2m |
C、若R足够大，质子的速度不可以被加速到任意值，因当达到一定速度后，质子的质量发生变化，导致周期变化，故C错误；
D、若是α粒子，则粒子的比荷发生变化，所以周期也变化，因此不能用这个装置，故D错误，
故选AB．
点评：解决本题的关键知道根据qvB=m
可求出最大速度，以及知道最大动能与D形盒的半径和磁感应强度的大小有关．
| v2 |
| R |
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
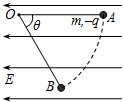（2006?淮安二模）如图所示，在场强大小为E的匀强电场中，一根不可伸长的绝缘细线一端拴一个质量为m电荷量为q的带负电小球，另一端固定在O点．把小球拉到使细线水平的位置A，然后将小球由静止释放，小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零．以下说法正确的是（ ）
（2006?淮安二模）如图所示，一根不可伸长的轻绳一端拴着一个小球，另一端固定在竖直杆上，当竖直杆以角速度ω转动时，小球跟着杆一起做匀速圆周运动，此时绳与竖直方向的夹角为θ，下列关于ω与θ关系的图象正确的是（ ）