题目内容
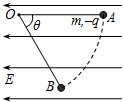（2006?淮安二模）如图所示，在场强大小为E的匀强电场中，一根不可伸长的绝缘细线一端拴一个质量为m电荷量为q的带负电小球，另一端固定在O点．把小球拉到使细线水平的位置A，然后将小球由静止释放，小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零．以下说法正确的是（ ）分析：类比单摆，小球从A点静止释放，运动到B点速度为0，说明弧AB的中点是运动的最低点，对小球进行受力分析，小球处在弧线中点位置时切线方向合力为零，再根据几何关系可以求出Eq，球到达B点时速度为零，向心力为零，则沿细线方向合力为零，此时对小球受力分析，再根据几何关系即可解题．
解答：解：（1）类比单摆，根据对称性可知，小球处在弧线中点位置时切线方向合力为零，此时细线与水平方向夹角恰为30°，根据三角函数关系可得：qEsin30°=mgcos30°，化简可知Eq=
mg，选项A错误、B正确；
（2）小球到达B点时速度为零，向心力为零，则沿细线方向合力为零，此时对小球受力分析可知：T=qEcos60°+mgsin60°，故细线拉力T=
mg，选项C正确、D错误．
故选BC．
| 3 |
（2）小球到达B点时速度为零，向心力为零，则沿细线方向合力为零，此时对小球受力分析可知：T=qEcos60°+mgsin60°，故细线拉力T=
| 3 |
故选BC．
点评：本题要求同学们能正确进行受力，并能联想到已学的物理模型，根据相关公式解题．
练习册系列答案
阅读快车系列答案
相关题目
（2006?淮安二模）如图所示，一根不可伸长的轻绳一端拴着一个小球，另一端固定在竖直杆上，当竖直杆以角速度ω转动时，小球跟着杆一起做匀速圆周运动，此时绳与竖直方向的夹角为θ，下列关于ω与θ关系的图象正确的是（ ）