题目内容
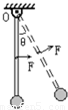
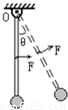
如图所示,一轻杆上端可以绕固定的水平轴O无摩擦转动,轻杆下端固定一个质量为m的小球(可视为质点),开始时轻杆竖直静止.现用力F=mg垂直作用于轻杆的中点,使轻杆转动,转动过程保持力F与轻杆垂直,当轻杆转过的角度θ=______时,质点m的速度最大.若从轻杆竖直静止开始保持F=mg,且始终水平作用于轻杆的中点,则杆能转过的最大角度θm=______.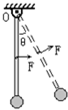

(1)力F=mg垂直作用于轻杆的中点,当轻杆转过的角度θ时,重力力矩等于F力矩,此时速度最大,
则有:
mgL=mgLsinθ
解得sinθ=
所以θ=30°
(2)杆转到最大角度时,速度为零,根据动能定理得:
mv2=
FL-mgLsinθ
所以
FLsinθ-mgL(1-cosθ)=0-0
即:
mgLsinθ-mgL(1-cosθ)=0
解得:θ=53°
故答案为:30°;53°
则有:
| 1 |
| 2 |
解得sinθ=
| 1 |
| 2 |
所以θ=30°
(2)杆转到最大角度时,速度为零,根据动能定理得:
| 1 |
| 2 |
| 1 |
| 2 |
所以
| 1 |
| 2 |
即:
| 1 |
| 2 |
解得:θ=53°
故答案为:30°;53°

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013?闵行区二模)如图所示,一轻杆上端可以绕固定的水平轴O无摩擦转动,轻杆下端固定一个质量为m的小球(可视为质点),开始时轻杆竖直静止.现用力F=mg垂直作用于轻杆的中点,使轻杆转动,转动过程保持力F与轻杆垂直,当轻杆转过的角度θ=
(2013?闵行区二模)如图所示,一轻杆上端可以绕固定的水平轴O无摩擦转动,轻杆下端固定一个质量为m的小球(可视为质点),开始时轻杆竖直静止.现用力F=mg垂直作用于轻杆的中点,使轻杆转动,转动过程保持力F与轻杆垂直,当轻杆转过的角度θ=