题目内容
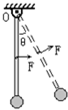
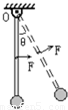
如图所示,一轻杆上端可以绕固定的水平轴O无摩擦转动,轻杆下端固定一个质量为m的小球(可视为质点),开始时轻杆竖直静止.现用力F=mg垂直作用于轻杆的中点,使轻杆转动,转动过程保持力F与轻杆垂直,当轻杆转过的角度θ= 时,质点m的速度最大.若从轻杆竖直静止开始保持F=mg,且始终水平作用于轻杆的中点,则杆能转过的最大角度θm= .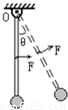
【答案】分析:(1)由题意可知:F始终对杆做正功,重力始终做负功,随着角度的增加重力做的负功运来越多,当重力力矩等于F力矩时速度达到最大值,此后重力做的负功比F做的正功多,速度减小;
(2)杆转到最大角度时,速度为零,根据动能定理即可求解.
解答:解:(1)力F=mg垂直作用于轻杆的中点,当轻杆转过的角度θ时,重力力矩等于F力矩,此时速度最大,
则有: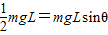
解得sinθ=
所以θ=30°
(2)杆转到最大角度时,速度为零,根据动能定理得:
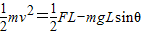
所以 =0-0
=0-0
即: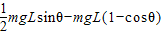 =0
=0
解得:θ=53°
故答案为:30°;53°
点评:本题主要考查了力矩和动能定理得直接应用,受力分析是解题的关键,难度适中.
(2)杆转到最大角度时,速度为零,根据动能定理即可求解.
解答:解:(1)力F=mg垂直作用于轻杆的中点,当轻杆转过的角度θ时,重力力矩等于F力矩,此时速度最大,
则有:
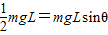
解得sinθ=

所以θ=30°
(2)杆转到最大角度时,速度为零,根据动能定理得:
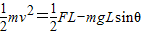
所以
 =0-0
=0-0即:
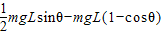 =0
=0解得:θ=53°
故答案为:30°;53°
点评:本题主要考查了力矩和动能定理得直接应用,受力分析是解题的关键,难度适中.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 (2013?闵行区二模)如图所示,一轻杆上端可以绕固定的水平轴O无摩擦转动,轻杆下端固定一个质量为m的小球(可视为质点),开始时轻杆竖直静止.现用力F=mg垂直作用于轻杆的中点,使轻杆转动,转动过程保持力F与轻杆垂直,当轻杆转过的角度θ=
(2013?闵行区二模)如图所示,一轻杆上端可以绕固定的水平轴O无摩擦转动,轻杆下端固定一个质量为m的小球(可视为质点),开始时轻杆竖直静止.现用力F=mg垂直作用于轻杆的中点,使轻杆转动,转动过程保持力F与轻杆垂直,当轻杆转过的角度θ=