ΧβΡΩΡΎ»ί
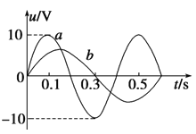
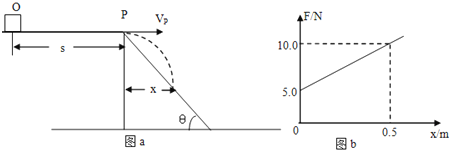
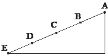
ΓΨΧβΡΩΓΩ»γΆΦΥυ Ψ,ΑκΨΕΈΣRΒΡΙβΜ§Ακ‘≤ΜΖΙλΒάABC”κ«ψΫ«Π»=37ΓψΒΡ¥÷≤Ύ–±ΟφΙλΒάCDœύ«–”ΎCΒψ,Ακ‘≤ΜΖΙλΒάΒΡ÷±ΨΕAC”κ–±ΟφΙλΒάCD¥Ι÷±ΓΘ÷ ΝΩΈΣmΒΡ–Γ«ρ¥”Ω’÷–Ρ≥ΒψΥ°ΤΫ≈Ή≥ωΚσ(¥ΥΒψΆΦ÷–ΟΜ”–±ξ≥ω),–Γ«ρΗ’ΚΟ”κΑκ‘≤ΜΖΙλΒάΒΡAΒψœύ«–Ϋχ»ΥΑκ‘≤ΜΖΙλΒάΡΎ≤ύ,–Γ«ρ‘ΥΕ·ΒΫΑκ‘≤ΜΖΙλΒάΉνΒΆΒψB¥Π ±Ε‘ΙλΒάΒΡ―ΙΝΠΈΣ6.6mg,÷°Κσ–Γ«ρ…œ…ΐΒΡΉν¥σΗΏΕ»Η’ΚΟΒ»”ΎΑκ‘≤ΜΖΙλΒάΒΡ÷±ΨΕΓΘ“―÷Σsin 37Γψ=0.6,cos 37Γψ=0.8,÷ΊΝΠΦ”ΥΌΕ»ΈΣg,Ω’ΤχΉηΝΠ≤ΜΦΤΓΘ«σ:
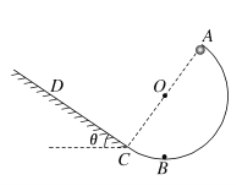
(1)–Γ«ρΥ°ΤΫ≈Ή≥ω ±ΒΡ≥θΥΌΕ»¥σ–Γ;
(2)–Γ«ρ”κ–±ΟφΙλΒάCD÷°ΦδΒΡΕ·ΡΠ≤Ν“ρ ΐΓΘ
ΓΨ¥πΑΗΓΩ(1) ![]() (2)
(2) ![]()
ΓΨΫβΈωΓΩ
(1)–Γ«ρ‘ΎΑκ‘≤ΜΖΙλΒάΉνΒΆΒψB¥Π ±Θ§”…≈ΘΕΌΒΎΕΰΕ®¬…ΒΟΘΚ
![]()
”…≈ΘΕΌΒΎ»ΐΕ®¬…ΒΟΘΚ
![]()
”…ΡήΝΩ ΊΚψΕ®¬…ΒΟΘΚ
![]()
ΗυΨίΦΗΚΈΙΊœΒΩ…ΒΟ–Γ«ρΥ°ΤΫ≈Ή≥ω ±ΒΡ≥θΥΌΕ»ΘΚ![]()
ΝΣΝΔΫβΒΟΘΚ
![]()
(2)…η–Γ«ρ‘Ύ–±ΟφΙλΒάCD…œ‘ΥΕ·ΒΡΨύάκΈΣsΘ§ΗυΨίΦΗΚΈΙΊœΒΒΟ
![]()
”…ΙΠΡήΙΊœΒΒΟΘΚ
![]()
ΝΣΝΔΫβΒΟΕ·ΡΠ≤Ν“ρ ΐΈΣ
![]()

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ