Question

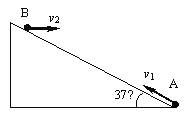
【题目】如图所示，质量m＝2 kg的小球用细绳拴在倾角θ＝37°的斜面上，g取10 m/s2，求：

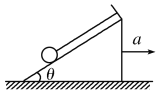
(1)当斜面以a1＝5 m/s2的加速度向右运动时，绳子拉力的大小；

(2)当斜面以a2＝20 m/s2的加速度向右运动时，绳子拉力的大小.

Answer 1

【答案】20N ；20

【解析】

首先判断小球是否飞离了斜面，根据小球刚刚飞离斜面的临界条件，即绳子的倾角不变，斜面的支持力刚好为零，解出此时的加速度与题目给出的加速度大小进行比较，若给出加速度大于小球的临界加速度说明小球已经飞离了斜面，否则小球还在斜面上；

解：设小球刚刚脱离斜面时，斜面向右的加速度为a0，此时斜面对小球的支持力恰好为零，小球只受重力和细绳的拉力，且细绳仍然与斜面平行，小球受力如图所示

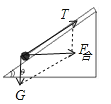
由牛顿第二定律得：

解得临界加速度：

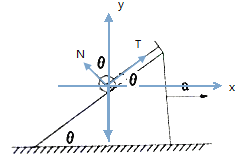
(1)加速度，则球压在斜面上，设球所受的支持力和绳子的拉力分别为N和T

根据牛顿第二定律得：

代入解得：

(2) ，则小球已离开斜面，绳子的拉力和重力的合力水平向右

则：