题目内容
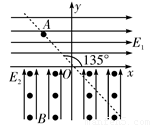
（15分）如图所示，直线OA与x轴成135°角，x轴上下方分别有水平向右的匀强电场E1和竖直向上的匀强电场E2，且电场强度E1＝E2＝10N/C，x轴下方还存在垂直于纸面向外的匀强磁场B，磁感应强度B＝10T。现有一质量m＝1.0×10－5kg，电荷量q＝1.0×10－5C的带正电尘粒在OA直线上的A点静止释放，A点离原点O的距离d＝
m(g取10m/s2，)．求：
(1)尘粒刚进入磁场区域时的速度v的大小；
(2)从进入磁场区域开始到离开磁场区域所经历的时间t；
(3)第一次回到OA直线上的某位置离原点O的距离L。
（1）2m/s（2）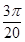
s（3）0.13m
解析试题分析：(1)F=Eq=1×10－4N ， 1分
尘粒在电场E中受到的合外力为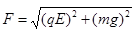
，1分
合外力F和水平方向间的夹角φ为tanφ＝
＝1
φ＝45°
尘粒在电场E1中的加速度a大小为a＝
g ， 2分
v＝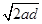
＝2m/s ，2分
(2)进入磁场后尘粒在磁场中转动的周期T和转动半径R分别为
T＝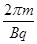
＝
s，2分
R＝
＝0.2m 2分
轨迹如图所示，由图可知，t＝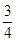
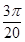T＝s 2分
(3)出磁场后尘粒在电场E1中做类平抛运动
OC＝R＝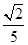
t1＝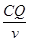
＝
＝
＝0.1s 2分
B位置离原点O的距离L大小为
L＝OC·sin45－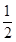
at1＝R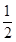－at1＝0.13m 2 分
考点：考查了粒子在电磁场中的综合应用
点评：电荷在匀强磁场中做匀速圆周运动，关键是画出轨迹，由几何知识求出半径．定圆心角，求时间．
练习册系列答案
相关题目
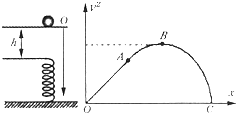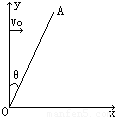
（2008?滨州一模）蹦床比赛中运动员从最高点下落过程可简化为下述物理模型．如图所示，劲度系数为k的轻弹簧竖直放置，下端固定在水平地面上，一质量为m的小球，从离弹簧上端高h处自由释放，压上弹簧后继续向下运动的过程中．若以小球开始下落的位置为原点，沿竖直向下建立坐标轴ox，则小球的速度平方随坐标x的变化图象如图所示，其中OA段为直线，ABC是平滑的曲线，AB段与OA相切于A点，关于A、B、C各点对应的位置坐标xA、xB、xC，及加速度aA、aB、aC的判断正确的是（ ）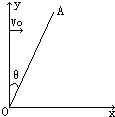
如图所示，直线OA与y轴成θ=30°角，在AOy范围内有沿y轴负方向的匀强电场，在AOx范围内有一个矩形区域的匀强磁场．该磁场区域的磁感应强度B=0.2T，方向垂直纸面向里．一带电微粒电荷量q=+2×10-14C，质量m=4×10-20kg，微粒子在y轴上的某点以速度v0垂直于y轴进入匀强电场，并以速度v=3×104m/s垂直穿过直线OA，运动中经过矩形磁场区域后，最终又垂直穿过x轴．不计微粒重力，求：（根据创新设计习题改编）
m(g取10m/s2，)．求：
