题目内容
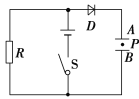
【题目】如图回旋加速器D形盒的半径为r，匀强磁场的磁感应强度为
一个质量了m、电荷量为q的粒子在加速器的中央从速度为零开始加速．
求该回旋加速器所加交变电场的频率；
求粒子离开回旋加速器时获得的动能；
设两D形盒间的加速电压为U，质子每次经电场加速后能量增加，加速到上述能量所需时间
不计在电场中的加速时间
．
【答案】（1）
（2）
（3）
【解析】
试题分析: （1）由回旋加速器的工作原理知，交变电场的频率与粒子在磁场运动的频率相等，故:
粒子在磁场中做匀速圆周运动过程，洛伦兹力提供向心力，根据牛顿第二定律，有：
周期：
联立解得：
，
(2)粒子离开磁场时速度最大，根据牛顿第二定律，有：
最大动能：
联立解得：
（3）加速次数：
粒子每转动一圈加速两次，故转动的圈数为：
粒子运动的时间为：t=nT
联立解得：
练习册系列答案
相关题目
