��Ŀ����
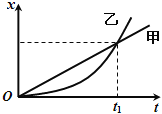
����Ŀ����ͼ��ʾ����ֱ������һԲ��С��Ȧ�����Ե���ȴ�����Բ��ͬ�ķ��á�����Բ���Ĵ�����ΪQ����Բ����Բ���˶�������ٶ�����ʱ��t�ı仯��ϵ��ͼ����ʾ(ͼ����0��t1��t2Ϊ��֪��)����Ȧͨ����Ե��������������ֱ�ļ��Ϊl�Ĺ⻬ƽ�н��������죬�������ľ��������ڴ��ڴ�ֱֽ�������ˮƽ��ǿ�ų����ų������±߽���Ϊh���Ÿ�Ӧǿ�ȴ�С��ΪB�����������ι����ɾ�Ե�˹������ΪH(H��h)��ˮƽ������AB��CD��ɣ����뵼����ܽӴ�����ʼʱ�������������ι��ܣ�ʹAB��λ�ڴų��ڵ��ϱ��أ�t1ʱ�̽��������t2ʱ�̿�ʼ�˶�����֪���������ι��ܵ�����Ϊm��AB����CD���뿪�ų��±���ʱ���ٶȴ�С��Ϊv��������AB��CD��Բ����Ȧ�ĵ����ΪR��������費�ƣ���������Ȧ���ԸС���

(1)0-t1ʱ���ڣ�����Բ���ĵ�Ч������
(2)t1-t2ʱ���ڣ�Բ����Ȧ��ͨ���仯�ʵĴ�С�����жϴ���Բ��Բ���˶�����(˳ʱ�뻹����ʱ�뷽��?)��
(3)��0ʱ�̵�CD���뿪�ų���ȫ����AB���ϲ����Ľ����ȡ�
���𰸡�(1)![]() ��(2)
��(2) ![]() ������Բ��Բ���˶�����Ϊ��ʱ�뷽����(3)
������Բ��Բ���˶�����Ϊ��ʱ�뷽����(3) ![]()
��������
(1)�ɵ����Ķ���ʽ��֪��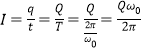 ��
��
(2) t1-t2ʱ���ڣ� ���������ι��ܴ���ƽ��״̬����ƽ��������֪��
![]()
��ã�![]()
��ŷķ���ɿ�֪��
![]()
��ã�![]()
��AB������ƽ���֪��AB���еĵ���������A��B��СԲ����Ȧ�еĵ�������Ϊ��ʱ�뷽���ɡ���ζ��ɡ��е�������ͬ��֪������Բ��Բ���˶�����Ϊ��ʱ�뷽��
(3)�ɹ��ܹ�ϵ��֪��![]()
�ɵ�·�ص��֪��![]()
��������ʽ��ã�![]()