题目内容
 一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量△ω与对应之间△t的比值定义为角加速度β(即ρ=
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量△ω与对应之间△t的比值定义为角加速度β(即ρ=| △? | △t |
①如图甲所示,将打点计时器固定在桌面上,将纸带的一端穿过打点计时器的限位孔,然后固定在圆盘的侧面,当圆盘转动时,纸带可以卷在圆盘侧面上;
②接通电源,打点计时器开始打点,启动控制装置使圆盘匀加速转动;
③经过一段时间,停止转动和打点,取下纸带,进行测量.
(1)用20分度的游标卡尺测得圆盘的半径如图乙所示,圆盘的半径r为
6.000
6.000
cm;(2)由图丙可知,打下计数点D时,圆盘转动的角速度为
6.5
6.5
rad/s;(3)纸带运动的加速度大小为
0.59
0.59
m/s2,圆盘转动的角加速度大小为9.8
9.8
rad/s2;(4)如果实验测出的角加速度值偏大,其原因可能是
测量转动半径时没有考虑纸带的厚度
测量转动半径时没有考虑纸带的厚度
(至少写出1条).分析:(1)20分度的游标卡尺精确度为0.05mm,读数时先读大于1mm的整数部分,再读不足1m的小数部分;
(2)根据平均速度等于中间时刻瞬时速度求出D点的瞬时速度,然后根据v=ωr求解角速度;
(3)用逐差法求解出加速度,再根据加速度等于角加速度与半径的乘积来计算角加速度;
(4)根据公式ρ=ar进行判断.
(2)根据平均速度等于中间时刻瞬时速度求出D点的瞬时速度,然后根据v=ωr求解角速度;
(3)用逐差法求解出加速度,再根据加速度等于角加速度与半径的乘积来计算角加速度;
(4)根据公式ρ=ar进行判断.
解答:解:(1)整数部分为60mm,小数部分为零,由于精确度为0.05mm,故需写到0.001cm处,故读数为6.000cm;
故答案为:6.000;
(2)打下计数点D时,速度为
vD=
=
=0.389m/s
故
ω=
=
≈6.5rad/s
故答案为:6.5;
(3)纸带运动的加速度为
a=
=
=
=0.59m/s2
由于ρ=
,ω=
,故角加速度为ρ=
=
≈9.8rad/s2
故答案为:0.59,9.8;
(4)根据公式ρ=
,ρ偏大,为a偏大,或者r偏小,故可能的原因为:测量转动半径时没有考虑纸带的厚度.
故答案为:6.000;
(2)打下计数点D时,速度为
vD=
| CE |
| 2T |
| (13.19-5.41)×0.01 |
| 2×0.1s |
故
ω=
| v |
| r |
| 0.389 |
| 0.06 |
故答案为:6.5;
(3)纸带运动的加速度为
a=
| △x |
| (△t)2 |
| CE-AC |
| (△t)2 |
| (13.19-2×5.41)×0.01 |
| 0.22 |
由于ρ=
| △? |
| △t |
| v |
| r |
| a |
| r |
| 0.59 |
| 0.06 |
故答案为:0.59,9.8;
(4)根据公式ρ=
| a |
| r |
点评:本题根据根据题意中角加速度的定义,同时结合纸带处理中加速度和速度的求法进行分析处理.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
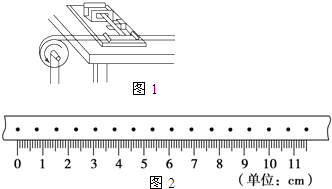 一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动.用下面的方法测量它匀速转动时的角速度.
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动.用下面的方法测量它匀速转动时的角速度.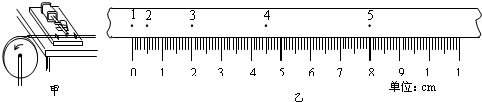
 一个有一定厚度的圆盘A,可以绕通过中心垂直于盘面的水平轴转动.用下面的方法测量它匀速转动的角速度.
一个有一定厚度的圆盘A,可以绕通过中心垂直于盘面的水平轴转动.用下面的方法测量它匀速转动的角速度.