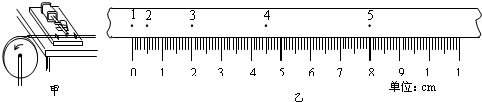
题目内容
 一个有一定厚度的圆盘A,可以绕通过中心垂直于盘面的水平轴转动.用下面的方法测量它匀速转动的角速度.
一个有一定厚度的圆盘A,可以绕通过中心垂直于盘面的水平轴转动.用下面的方法测量它匀速转动的角速度.实验器材:电磁打点计时器,米尺,纸带,复写纸片.
实验步骤:
(1)如图所示,将电磁打点计时器固定在桌面上,将纸带的一端穿过打点计时器的限位孔后,固定在待测圆盘的侧面上,使得圆盘转动时,纸带可以卷在圆盘侧面上.
(2)启动控制装置使圆盘转动,同时接通电源,打点计时器开始打点.
(3)经过一段时间,停止转动和打点,取下纸带,进行测量(已知电磁打点计时器打点周期为T).需要测量的物理量有
分析:通过纸带打点的时间间隔和位移,求出圆盘的线速度,根据ω=
得出角速度的表达式,代入数据求出角速度的大小.
| v |
| r |
解答:解:要先求出角速度,比先求出线速度,由于是用纸带测量圆盘的线速度,再利用ω=
得出角速度,所以需要测盘的半径r,n个点之间的间距x.
在纸带上取两点为n个打点周期,距离为x,则圆盘的线速度为:v=
得:ω=
=
故答案为:盘的半径r,n个点之间的间距x;
.
| v |
| r |
在纸带上取两点为n个打点周期,距离为x,则圆盘的线速度为:v=
| x |
| (n-1)T |
得:ω=
| v |
| r |
| x |
| (n-1)Tr |
故答案为:盘的半径r,n个点之间的间距x;
| x |
| (n-1)Tr |
点评:解决本题的关键知道该实验的原理,通过纸带处理求出圆盘的线速度,根据线速度与角速度的关系,求出角速度的表达式.

练习册系列答案
相关题目
 一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量△ω与对应时间△t的比值定义为角加速度β.我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验:(打点计时器所接交流电的频率为50Hz,A、B、C、D…为计数点,相邻两计数点间有四个点未画出)
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量△ω与对应时间△t的比值定义为角加速度β.我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验:(打点计时器所接交流电的频率为50Hz,A、B、C、D…为计数点,相邻两计数点间有四个点未画出)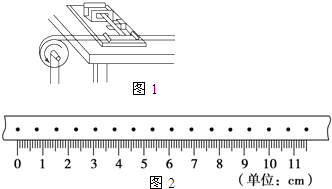 一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动.用下面的方法测量它匀速转动时的角速度.
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动.用下面的方法测量它匀速转动时的角速度.