题目内容
15.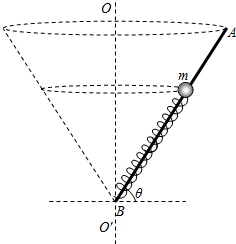 如图所示,光滑杆AB长为L,B端固定一根劲度系数为k,原长为l0的轻弹簧,质量为m的小球套在光滑杆上并与弹簧的上端连接,OO′为过B点的竖直轴,杆与水平面间的夹角始终为θ.
如图所示,光滑杆AB长为L,B端固定一根劲度系数为k,原长为l0的轻弹簧,质量为m的小球套在光滑杆上并与弹簧的上端连接,OO′为过B点的竖直轴,杆与水平面间的夹角始终为θ.(1)杆保持静止状态,让小球从弹簧的原长位置静止释放,求小球释放瞬间的加速度大小a及小球速度最大时弹簧的压缩量△l1;
(2)当球随杆一起绕OO′轴匀速转动时,弹簧伸长量为△l2,求匀速转动的角速度ω;
(3)若θ=30°,移去弹簧,当杆绕OO′轴以角速度ω0=$\sqrt{\frac{g}{L}}$匀速转动时,小球恰好在杆上某一位置随杆在水平面内匀速转动,球受轻微扰动后沿杆向上滑动,到最高点A时求沿杆方向的速度大小为v0,求小球从开始滑动到离开杆过程中,杆对球所做的功W.
分析 (1)根据牛顿第二定律求出小球释放瞬间的加速度大小,当小球的加速度为零时,速度最大,结合平衡求出弹簧的压缩量.
(2)对小球分析,抓住竖直方向上的合力为零,水平方向上的合力提供向心力,列式联立求出匀速转动的角速度.
(3)根据牛顿第二定律求出小球做匀速转动时距离B点的距离,求出此时小球的动能,结合最高点的动能,运用动能定理求出杆对小球做功的大小.
解答 解:(1)小球释放的瞬间,小球的加速度大小为:a=$\frac{mgsinθ}{m}=gsinθ$,
当小球速度相等时,有:mgsinθ=k△l1,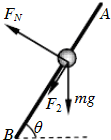
解得弹簧的压缩量为:$△{l}_{1}=\frac{mgsinθ}{k}$
(2)当弹簧伸长量为△l2,受力如图所示,在水平方向上有:
${F}_{N}sinθ+k△{l}_{2}cosθ=m{ω}^{2}$(l0+△l2)cosθ,
竖直方向上有:FNcosθ-k△l2sinθ-mg=0,
解得:$ω=\sqrt{\frac{mgsinθ+k△{l}_{2}}{m({l}_{0}+△{l}_{2})co{s}^{2}θ}}$.
(3)当杆绕OO′轴以角速度ω0匀速转动时,设小球距离B点L0,此时有:
$mgtanθ=m{{ω}_{0}}^{2}{L}_{0}cosθ$,
解得:${L}_{0}=\frac{2L}{3}$.
此时小球的动能为:${E}_{k0}=\frac{1}{2}m({ω}_{0}{L}_{0}cosθ)^{2}$.
小球在最高点A离开杆瞬间的动能为:${E}_{kA}=\frac{1}{2}m[{{v}_{0}}^{2}+({ω}_{0}Lcosθ)^{2}]$.
根据动能定理有:W-mg(L-L0)sinθ=EkA-Ek0,
解得:W=$\frac{3}{8}mgL+\frac{1}{2}m{{v}_{0}}^{2}$.
答:(1)小球释放瞬间的加速度大小a为gsinθ,小球速度最大时弹簧的压缩量△l1为$\frac{mgsinθ}{k}$.
(2)匀速转动的角速度为$\sqrt{\frac{mgsinθ+k△{l}_{2}}{m({l}_{0}+△{l}_{2})co{s}^{2}θ}}$.
(3)杆对球所做的功为$\frac{3}{8}mgL+\frac{1}{2}m{{v}_{0}}^{2}$.
点评 本题考查了动能定理、牛顿第二定律、胡克定律与圆周运动的综合,知道小球做匀速转动时,靠径向的合力提供向心力,由静止释放时,加速度为零时速度最大.

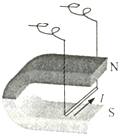 探究影响安培力大小因素的实验装置如图所示,直导线垂直磁场方向置于磁场中某处.当导线中电流为I时,导线所受安培力大小为F;现仅将导线中电流减小为$\frac{I}{2}$时,导线所受安培力大小为( )
探究影响安培力大小因素的实验装置如图所示,直导线垂直磁场方向置于磁场中某处.当导线中电流为I时,导线所受安培力大小为F;现仅将导线中电流减小为$\frac{I}{2}$时,导线所受安培力大小为( )| A. | 2F | B. | F | C. | $\frac{F}{2}$ | D. | $\frac{F}{4}$ |

| A. | 斜面对物块的支持力一定变小 | B. | 斜面对物块的支持力一定变大 | ||
| C. | 斜面对物块的静摩擦力一定变小 | D. | 斜面对物块的静摩擦力一定变大 |
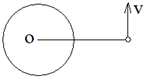 库仑定律是电学中第一个被发现的定量规律,它的发现受万有引力定律的启发.实际问题中有时需要同时考虑万有引力和库仑力,比如某无大气层的均匀带有大量负电荷的质量分布均匀的星球.将一个带电微粒置于离该星球表面一定高度处无初速释放,发现微粒恰好能静止.现给微粒一个如图所示的初速度v,则下列说法正确的是( )
库仑定律是电学中第一个被发现的定量规律,它的发现受万有引力定律的启发.实际问题中有时需要同时考虑万有引力和库仑力,比如某无大气层的均匀带有大量负电荷的质量分布均匀的星球.将一个带电微粒置于离该星球表面一定高度处无初速释放,发现微粒恰好能静止.现给微粒一个如图所示的初速度v,则下列说法正确的是( )| A. | 微粒将做匀速直线运动 | B. | 微粒将做圆周运动 | ||
| C. | 库仑力对微粒做正功 | D. | 万有引力对微粒做正功 |
 如图所示,甲、乙两个质量相同、带等量异种电荷的带电粒子,以不同的速率经小孔P从磁场边界MN,进入方向垂直纸面向里的匀强磁场中,在磁场中作匀速圆周运动,并垂直磁场边界MN射出磁场,半圆轨迹如图中虚线所示,不计粒子所受的重力及空气阻力,则下列说法中正确的是( )
如图所示,甲、乙两个质量相同、带等量异种电荷的带电粒子,以不同的速率经小孔P从磁场边界MN,进入方向垂直纸面向里的匀强磁场中,在磁场中作匀速圆周运动,并垂直磁场边界MN射出磁场,半圆轨迹如图中虚线所示,不计粒子所受的重力及空气阻力,则下列说法中正确的是( )| A. | 甲带负电荷,乙带正电荷 | |
| B. | 洛伦兹力对甲做功 | |
| C. | 甲的速率大于乙的速率 | |
| D. | 甲在磁场中运动的时间大于乙在磁场中运动的时间 |