Question

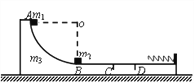
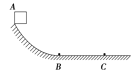
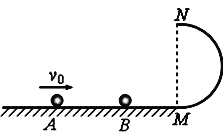
【题目】在光滑的水平面上，一质量为mA=0.1kg的小球A，以v0=9m/s的初速度向右运动，与质量为mB=0.2kg的静止小球B发生碰撞，碰撞时间极短，碰撞过程中没有机械能损失。碰后小球B滑向与水平面相切、半径为R的竖直放置的固定光滑半圆形轨道，且恰好能通过最高点N后水平抛出。重力加速度为g=10m/s2。求：

(1)碰撞后小球B的速度大小；

(2)圆轨道半径R的大小。

Answer 1

【答案】(1)6m/s (2)0.72m

【解析】

（1）由动量守恒定律可知：mAv0=mAv1+mBv2

由能量关系可知：

带入数据解得v2=6m/s

（2）小球B从轨道最低点M运动到最高点N的过程中机械能守恒，有：
mBv22=mBg2R+mBvN2

小球B恰好能通过圆形轨道最高点，有：mBg=mB

联立两式并带入数据解得R=0.72m