题目内容
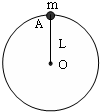 长度为L=0.5m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图,小球以O点为圆心在竖直平面内做圆周运动,g取10m/s2,计算下列各种情况小球对细杆OA的弹力.
长度为L=0.5m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图,小球以O点为圆心在竖直平面内做圆周运动,g取10m/s2,计算下列各种情况小球对细杆OA的弹力.(1)通过最低点时小球的速率是8.0m/s
(2)通过最高点时小球的速率是2.0m/s
(3)通过最高点时小球的速率是6.0m/s.
分析:物体运动到圆周运动的最低点时和最高点时,由杆的弹力和重力的合力提供向心力,可以直接根据牛顿第二定律列式求解.在最低点,杆对球有向上的拉力,在最高点时,杆对球的弹力可能向下,是拉力,也是向上,是支持力.
解答:解:
(1)小球通过最低点时,由杆的拉力和重力的合力提供向心力,根据牛顿第二定律得:
F1-mg=m
则得,F1=m(g+
)=3×(
+10)N=126N;
根据牛顿第三定律得:小球对细杆OA的弹力大小为126N,方向竖直向下.
(2)小球通过最高点时,假设杆对球的弹力向上,则由牛顿第二定律得:
mg-F2=m
解得,F2=m(g-
)=3×(10-
)N=6N>0,说明杆对球的弹力向上,是支持力;
根据牛顿第三定律得:小球对细杆OA的弹力大小为6N,方向竖直向下.
(3)小球通过最高点时,假设杆对球的弹力向上,则由牛顿第二定律得:
mg-F3=m
解得,F3=m(g-
)=3×(10-
)N=-186N<0,说明杆对球的弹力向下,是拉力;
根据牛顿第三定律得:小球对细杆OA的弹力大小为186N,方向竖直向上.
答:(1)通过最低点时小球的速率是8.0m/s时,小球对细杆OA的弹力大小为126N,方向竖直向下.
(2)通过最高点时小球的速率是2.0m/s,小球对细杆OA的弹力大小为6N,方向竖直向下.
(3)通过最高点时小球的速率是6.0m/s,小球对细杆OA的弹力大小为186N,方向竖直向上.
(1)小球通过最低点时,由杆的拉力和重力的合力提供向心力,根据牛顿第二定律得:
F1-mg=m
| ||
| L |
则得,F1=m(g+
| ||
| L |
| 82 |
| 0.5 |
根据牛顿第三定律得:小球对细杆OA的弹力大小为126N,方向竖直向下.
(2)小球通过最高点时,假设杆对球的弹力向上,则由牛顿第二定律得:
mg-F2=m
| ||
| L |
解得,F2=m(g-
| ||
| L |
| 22 |
| 0.5 |
根据牛顿第三定律得:小球对细杆OA的弹力大小为6N,方向竖直向下.
(3)小球通过最高点时,假设杆对球的弹力向上,则由牛顿第二定律得:
mg-F3=m
| ||
| L |
解得,F3=m(g-
| ||
| L |
| 62 |
| 0.5 |
根据牛顿第三定律得:小球对细杆OA的弹力大小为186N,方向竖直向上.
答:(1)通过最低点时小球的速率是8.0m/s时,小球对细杆OA的弹力大小为126N,方向竖直向下.
(2)通过最高点时小球的速率是2.0m/s,小球对细杆OA的弹力大小为6N,方向竖直向下.
(3)通过最高点时小球的速率是6.0m/s,小球对细杆OA的弹力大小为186N,方向竖直向上.
点评:本题采用假设法,可先假设弹力向下,解的结果为正,假设成立,若为负,实际方向与假设方向相反.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
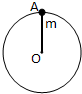 长度为L=0.5m的轻质杆OA,A端连有质量为m=4kg的小球,如图所示,小球以O点为圆心在竖直平面内作圆周运动,通过最高点时小球的速率为2m/s,取g=10m/s2,则此时细杆OA受到大小
长度为L=0.5m的轻质杆OA,A端连有质量为m=4kg的小球,如图所示,小球以O点为圆心在竖直平面内作圆周运动,通过最高点时小球的速率为2m/s,取g=10m/s2,则此时细杆OA受到大小 长度为L=0.5m的轻质细杆,一端固定有一质量为m=3kg的小球,小球以O点为圆心在竖直面内做圆周运动,小球通过最高点时速率为2m/s (g取10m/s2),则在最高点( )
长度为L=0.5m的轻质细杆,一端固定有一质量为m=3kg的小球,小球以O点为圆心在竖直面内做圆周运动,小球通过最高点时速率为2m/s (g取10m/s2),则在最高点( )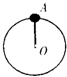 长度为L=0.5m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率为2.0m/s,不计空气阻力,g取10m/s2,则此时细杆OA受到( )
长度为L=0.5m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率为2.0m/s,不计空气阻力,g取10m/s2,则此时细杆OA受到( )